
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to Convert Binary to Decimal?
Binary is the simplest kind of number system that uses only two digits of 0 and 1 (i.e. value of base 2). Since digital electronics have only these two states (either 0 or 1), so binary number is most preferred in modern computer engineer, networking and communication specialists, and other professionals.
Whereas Decimal number is most familiar number system to the general public. It is base 10 which has only 10 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Conversion from Binary to Decimal number system
There are mainly two methods to convert a binary number into decimal number ? using positional notation, and using doubling. These methods are explained are as following below.
Using Positional Notation
Since number numbers are type of positional number system. That means weight of the positions from right to left are as 20, 21, 22, 23... and so on for the integer part and weight of the positions from left to right are as 2-1, 2-2, 2-3, 2-4... and so on for the fractional part.
| Most Significant Bit (MSB) | Binary Point | Least Significant Bit (LSB) | |||
|---|---|---|---|---|---|
| 22 | 21 | 20 | 2-1 | 2-2 | 2-3 |
| 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
Assume any unsigned binary number is bnb(n-1) ... b1b0.b-1b-2 ... b(m-1)bm. Then the decimal number is equal to the sum of binary digits (bn) times their power of 2 (2n), i.e., bnb(n-1) ... b1b0.b-1b-2 ... b(m-1)bm = bnx2n+b(n-1)x2(n-1)+ ... +b1x21+bx020+b-1x2-1+b-22-2+ ...
This is simple algorithm where you have to multiply positional value of binary with their digit and get the sum of these steps.
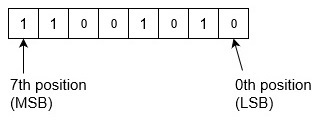
Example-1 ? Convert binary number 11001010 into decimal number. Since there is no binary point here and no fractional part. So,
Binary to decimal is,
= (11001010)2 = 1x27+1x26+0x25+0x24+1x23+0x22+1x21+0x20 = 128+64+0+0+8+0+2+0 = (202)10
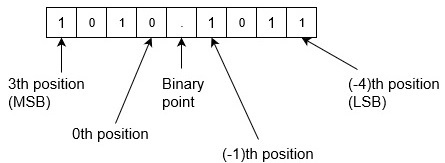
Example-2 ? Convert binary number 1010.1011 into decimal number. Since there is a binary point here with fractional part. So,
Binary to decimal is,
= (1010.1011)2 = 1x23+0x22+1x21+0x20+1x2-1+0x2-2+1x2-3+1x2-4 = 8+0+2+0+0.5+0+0.125+0.0625 = (10.6875)10
Using Doubling
This is simple method to convert a binary number into decimal number, you need to start from leftmost digit (or MSB) from the input. Take the most significant bit (MSB), right down, then multiply by 2 with it and add second leftmost bit, store it as current result, then again multiple by 2 with current result and add third leftmost bit, update this value as current result and follow this till addition of least significant bit (LSB or rightmost bit). Since you are doubling (multiplying by 2) each time, so this method is known as Doubling.
These are simple algorithm is explained below in steps ?
Write down the binary number.
Starting from the left, double your previous total and add the current digit.
Double your current total and add the next leftmost digit.
Repeat the previous step.
For example, Convert binary number 11101110 into decimal number. According to above algorithm, Binary to decimal is,
= (11101110)2 = 1 = 12+1 =3 = 32+1=7 = 72+0=14 = 142+1=29 = 292+1=59 = 592+1=119 = 1192+0=238 = (238)10
These are above two simple methods to convert a binary number into decimal number.

