Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How do Power Stations produce more kW when there is an increased demand?
The useful output of a power generating station is the kW output which is delivered by the station to the electrical supply system. Sometimes, a power generating station needs to deliver more kW to meet the increased power demand. This can be achieved by any of the following two methods −
By increasing kVA capacity – In this method, the kVA capacity of the power generating station is increased at the same power factor to meet the increased kW demand. Although, this causes extra cost to increase the kVA capacity of the power station.
By improving power factor – In this method, the power factor of the power station is improved, say from $\mathrm{cos}\, \phi _{\mathrm{1}}$ to $\mathrm{cos}\, \phi _{\mathrm{2}}$, without increasing the kVA capacity of the power station to meet the increased kW demand. It also results in extra cost on account of power factor correction equipment.
Economical Comparison of the Two Methods
As from the definition of two methods for meeting the increased kW demand on power station, it is clear that each method involves extra cost. Therefore, we need to make economical comparison of two methods.
Consider a power station of rating S kVA is supplying the load at power factor $\mathrm{cos}\, \phi _{\mathrm{1}}$. As we know, the increased power demand can be met either by improving the power factor from $\mathrm{cos}\, \phi _{\mathrm{1}}$ to $\mathrm{cos}\, \phi _{\mathrm{2}}$ at S kVA or by increasing the kVA rating of the station at the original power factor $\mathrm{cos}\, \phi _{\mathrm{1}}$.
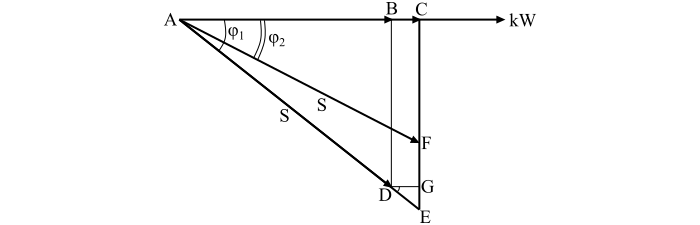
Cost of Increasing kVA Capacity of Power Station
Refer the power triangle shown in the figure. The increased kVA capacity of the power station at the original power factor $\mathrm{cos}\, \phi _{\mathrm{1}}$ to meet the increased kW demand is given by,
$$\mathrm{Increased \: kVA \: Capacity\: \mathit{\mathrm{\, =\, }DE\mathrm{\, =\, }\frac{DG}{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }\frac{BC}{\mathrm{cos}\, \phi _{\mathrm{1}}};\; \; \; \left ( \because DG\mathrm{\, =\, }BC \right )}}$$
$$\mathrm{\Rightarrow Increased\: kVA \: Capacity\mathit{\mathrm{\, =\, }\frac{AC-AB}{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }\frac{AF\,\mathrm{cos}\, \phi _{\mathrm{2}}-AD\,\mathrm{cos}\, \phi _{\mathrm{1}} }{\mathrm{cos}\, \phi _{\mathrm{1}}}}}$$
$$\mathrm{\Rightarrow Increased\: kVA \: Capacity \mathit{\mathrm{\, =\, }\frac{S\left ( \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{cos}\, \phi _{\mathrm{1}} \right )}{\mathrm{cos}\, \phi _{\mathrm{1}}};\; \; \left ( \because AF\mathrm{\, =\, }AD\mathrm{\, =\, }S \right )}}$$
Now, let Rs. x is the cost per kVA per annum of the power station, then the cost per annum due to increased kVA capacity is
$$\mathrm{Annual \: cost\: due\: to\: increased\: kVA\: capacity \mathit{\mathrm{\, =\, }Rs.x\left [ \frac{S\left ( \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{cos}\, \phi _{\mathrm{1}} \right )}{\mathrm{cos}\, \phi _{\mathrm{1}}} \right ] }}$$
Cost of Power Factor Correction Equipment
The increased kW demand can be met by improving the power factor from $\mathrm{cos}\, \phi _{\mathrm{1}}$ to $\mathrm{cos}\, \phi _{\mathrm{2}}$ without increasing the kVA capacity of the power station.
Refer the power triangle given in the above figure, the leading kVAR to be taken by the power factor correction equipment is given by,
$$\mathrm{Leading\: kVAR \mathit{\mathrm{\, =\, }FE\mathrm{\, =\, }CE-CF}}$$
$$\mathrm{\Rightarrow Leading\: kVAR \mathit{\mathrm{\, =\, }AE\, \mathrm{sin}\, \phi _{\mathrm{1}}-AF\, \mathrm{sin}\, \phi _{\mathrm{2}}}}$$
$$\mathrm{\Rightarrow Leading\: kVAR \mathit{\mathrm{\, =\, }\frac{AC}{\mathrm{cos}\, \phi _{\mathrm{1}}}\, \mathrm{sin}\, \phi _{\mathrm{1}}-AF\, \mathrm{sin}\, \phi _{\mathrm{2}}}}$$
$$\mathrm{\Rightarrow Leading\: kVAR\mathit{\mathrm{\, =\, }\frac{AF\, \mathrm{cos}\, \phi _{\mathrm{2}}}{\mathrm{cos}\, \phi _{\mathrm{1}}}\, \mathrm{sin}\, \phi _{\mathrm{1}}-AF\, \mathrm{sin}\, \phi _{\mathrm{2}}}}$$
$$\mathrm{\Rightarrow Leading\: kVAR \mathit{\mathrm{\, =\, }AF\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$
$$\mathrm{\therefore Leading\: kVAR \mathit{\mathrm{\, =\, }S\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$
Now, let Rs. y is the cost per kVAR per annum of the power factor correction equipment, then the annual cost of the power factor correction equipment is
$$\mathrm{Cost\: of\: pf\: correction\: equipment\mathit{\, \mathrm{\, =\, }\, Rs.y\, S\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$
Numerical Example
A power station is working at its maximum kVA capacity with a power factor 0.75 lagging. It is now required to increase its kW capacity to meet the increased load demand. This can be done by,
Installing an additional power station costing Rs 850 per kVA, or
Increasing the power factor to 0.85 lagging by installing a power factor correction equipment.
What is the maximum cost per kVA of power factor correction equipment to make its use more economical then the addition power station?
Solution
Let the initial kVA capacity of the power station is S kVA at power factor $\mathrm{cos}\, \phi _{\mathrm{1}}$.
Cost of increasing kVA Capacity –
$$\mathrm{Cost\: of\: increasing\: kVA\: capacity \mathit{\mathrm{\, =\, }Rs.}850\times \left [ \frac{\mathit{S}\left ( 0.85-0.75 \right )}{0.75} \right ]}$$
$$\mathrm{Cost\: of\: increasing\: kVA \:capacity \mathit{\mathrm{\, =\, }Rs.}113.33\times \mathit{S}\; \; \cdot \cdot \cdot \left ( 1 \right )}$$
Cost of power factor correction equipment –
The power factor angles $\mathrm{\phi _{1}}$ and $\mathrm{\phi _{2}}$ are given by,
$$\mathrm{\phi _{1}\, =\, cos^{-1}\, 0.75\, =\,41.41^{\circ }\: and\: \phi _{2}\, =\, cos^{-1}\, 0.85\, =\,31.78^{\circ }}$$
$$\mathrm{\therefore Cost\: of\: pf\: correction\: equipment\mathit{\, \mathrm{\, =\, }\, \mathrm{Rs}.y\, S\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$
$$\mathrm{\Rightarrow Cost\: of\: pf\: correction\: equipment\mathit{\, \mathrm{\, =\, }\, \mathrm{Rs}.y\,\times S\times \left ( \mathrm{tan\, 41.41^{\circ }\times 0.85}-\mathrm{sin\, 31.78^{\circ }}\, \right )}}$$
$$\mathrm{\therefore Cost\: of\: pf\: correction\: equipment\mathit{\, \mathrm{\, =\, }\, \mathrm{Rs.\, 0.223}\times y\times S\; \; \; \cdot \cdot \cdot }\left ( 2 \right )}$$
The cost of per kVA of the power factor correction that would justify its installation is when eqns. (1) and (2) are equal, i.e.,
$$\mathrm{113.33 \times \mathit{S}\, \mathrm{\, =\, }\, 0.223 \times \mathit{y} \times \mathit{S}}$$
$$\mathrm{\mathit{\Rightarrow y}\mathrm{\, =\, }\frac{113.33}{0.223}\mathrm{\, =\, }Rs. 508.2\, per\, kVAR}$$
When the power factor correction equipment is ideal, then its kVAR = kVA. Therefore, the maximum cost per kVA of power factor correction equipment is Rs 508.2.
370 Views
