Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Generic Methods for DEPQs
Dual Heap
Existence of general methods to arrive at efficient DEPQ (Double Ended Priority Queue) data structures from single-ended priority queue (PQ) data structures that also provide an efficient implementation of the remove(aNode) operation (this operation eliminates the node aNode from the PQ). The simplest of these methods, dual structure method, keeps track of both a min PQ and a max PQ of all the DEPQ elements associated with correspondence pointers between the nodes of the min PQ and the max PQ consisting the same element.
Figure A displays a dual heap structure for the elements 7, 8, 3, 6, 5. Correspondence pointers are displayed as red arrows.
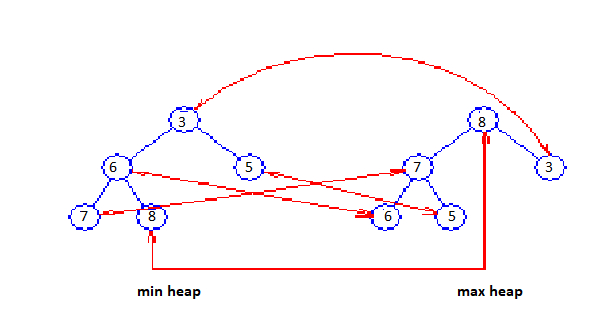
Figure A: Dual heap
Although the figure displays each element stored in both the min and the max heap, it is required to store each element in only one of the two heaps.
The isEmpty and size operations are applied by implementing a variable size that keeps track of the number of elements in the DEPQ. The minimum element is located at the root of the min heap and the maximum element is located at the root of the max heap. To insert an element A, we insert A into both the min and the max heaps and then set up correspondence pointers between the locations of A in the min and max heaps. To eliminate the minimum element, we do a removeMin from the min heap and a remove(aNode), where aNode is the corresponding node for the removed element, from the max heap. The maximum element is eliminated in an analogous way.
Total and leaf correspondence
Total and leaf correspondence are more sophisticated correspondence techniques. In both of these techniques, half the elements are located in the min PQ and the other half in the max PQ. When the number of elements is odd, one element is stored in a buffer. This buffered element is not the member of either PQ. In total correspondence technique, each element x in the min PQ is paired with a distinct element y of the max PQ. (x, y) is a corresponding pair of elements such that priority(x) <= priority(y).
Figure B displays a total correspondence heap for the 11 elements 3, 4, 5, 5, 6, 6, 7, 8, 9, 10, 11. The element 10 is in the buffer. Corresponding pairs are displayed by red arrows.
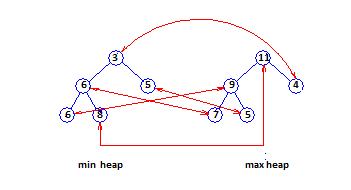
Figure B: Total correspondence heap
In leaf correspondence technique, each leaf element of the min and max PQ is needed to be part of a corresponding pair. Nonleaf elements do not require to be in any corresponding pair. Figure C displays a leaf correspondence heap.
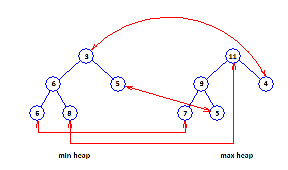
Figure C: A leaf correspondence heap
Total and leaf correspondence structures need less space than dual structures. However, the DEPQ Algorithms for total and leaf correspondence structures are more complicated than those for dual structures. Of the three correspondence techniques, leaf correspondence be the fastest DEPQ correspondence structures.
Implementing any of the described correspondence techniques, we can arrive at DEPQ structures from heaps, height biased leftist trees, and pairing heaps. In these DEQP structures, the operations put(x), removeMin(), and removeMax() consume O(log n) time (n is the number of elements in the DEPQ, for pairing heaps, this is an amortized complexity), and the remaining DEPQ operations consume O(1) time.
79 Views
