
- Fuzzy Logic - Home
- Fuzzy Logic - Introduction
- Fuzzy Logic - Classical Set Theory
- Fuzzy Logic - Set Theory
- Fuzzy Logic - Membership Function
- Traditional Fuzzy Refresher
- Approximate Reasoning
- Fuzzy Logic - Inference System
- Fuzzy Logic - Database and Queries
- Fuzzy Logic - Quantification
- Fuzzy Logic - Decision Making
- Fuzzy Logic - Control System
- Adaptive Fuzzy Controller
- Fuzziness in Neural Networks
- Fuzzy Logic - Applications
Fuzzy Logic - Quick Guide
Fuzzy Logic - Introduction
The word fuzzy refers to things which are not clear or are vague. Any event, process, or function that is changing continuously cannot always be defined as either true or false, which means that we need to define such activities in a Fuzzy manner.
What is Fuzzy Logic?
Fuzzy Logic resembles the human decision-making methodology. It deals with vague and imprecise information. This is gross oversimplification of the real-world problems and based on degrees of truth rather than usual true/false or 1/0 like Boolean logic.
Take a look at the following diagram. It shows that in fuzzy systems, the values are indicated by a number in the range from 0 to 1. Here 1.0 represents absolute truth and 0.0 represents absolute falseness. The number which indicates the value in fuzzy systems is called the truth value.
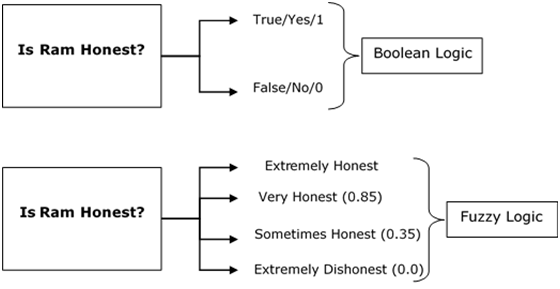
In other words, we can say that fuzzy logic is not logic that is fuzzy, but logic that is used to describe fuzziness. There can be numerous other examples like this with the help of which we can understand the concept of fuzzy logic.
Fuzzy Logic was introduced in 1965 by Lofti A. Zadeh in his research paper Fuzzy Sets. He is considered as the father of Fuzzy Logic.
Fuzzy Logic - Classical Set Theory
A set is an unordered collection of different elements. It can be written explicitly by listing its elements using the set bracket. If the order of the elements is changed or any element of a set is repeated, it does not make any changes in the set.
Example
- A set of all positive integers.
- A set of all the planets in the solar system.
- A set of all the states in India.
- A set of all the lowercase letters of the alphabet.
Mathematical Representation of a Set
Sets can be represented in two ways −
Roster or Tabular Form
In this form, a set is represented by listing all the elements comprising it. The elements are enclosed within braces and separated by commas.
Following are the examples of set in Roster or Tabular Form −
- Set of vowels in English alphabet, A = {a,e,i,o,u}
- Set of odd numbers less than 10, B = {1,3,5,7,9}
Set Builder Notation
In this form, the set is defined by specifying a property that elements of the set have in common. The set is described as A = {x:p(x)}
Example 1 − The set {a,e,i,o,u} is written as
A = {x:x is a vowel in English alphabet}
Example 2 − The set {1,3,5,7,9} is written as
B = {x:1 ≤ x < 10 and (x%2) ≠ 0}
If an element x is a member of any set S, it is denoted by x∈S and if an element y is not a member of set S, it is denoted by y∉S.
Example − If S = {1,1.2,1.7,2},1 ∈ S but 1.5 ∉ S
Cardinality of a Set
Cardinality of a set S, denoted by |S||S|, is the number of elements of the set. The number is also referred as the cardinal number. If a set has an infinite number of elements, its cardinality is ∞∞.
Example − |{1,4,3,5}| = 4,|{1,2,3,4,5,}| = ∞
If there are two sets X and Y, |X| = |Y| denotes two sets X and Y having same cardinality. It occurs when the number of elements in X is exactly equal to the number of elements in Y. In this case, there exists a bijective function f from X to Y.
|X| ≤ |Y| denotes that set Xs cardinality is less than or equal to set Ys cardinality. It occurs when the number of elements in X is less than or equal to that of Y. Here, there exists an injective function f from X to Y.
|X| < |Y| denotes that set Xs cardinality is less than set Ys cardinality. It occurs when the number of elements in X is less than that of Y. Here, the function f from X to Y is injective function but not bijective.
If |X| ≤ |Y| and |X| ≤ |Y| then |X| = |Y|. The sets X and Y are commonly referred as equivalent sets.
Types of Sets
Sets can be classified into many types; some of which are finite, infinite, subset, universal, proper, singleton set, etc.
Finite Set
A set which contains a definite number of elements is called a finite set.
Example − S = {x|x ∈ N and 70 > x > 50}
Infinite Set
A set which contains infinite number of elements is called an infinite set.
Example − S = {x|x ∈ N and x > 10}
Subset
A set X is a subset of set Y (Written as X ⊆ Y) if every element of X is an element of set Y.
Example 1 − Let, X = {1,2,3,4,5,6} and Y = {1,2}. Here set Y is a subset of set X as all the elements of set Y is in set X. Hence, we can write Y⊆X.
Example 2 − Let, X = {1,2,3} and Y = {1,2,3}. Here set Y is a subset (not a proper subset) of set X as all the elements of set Y is in set X. Hence, we can write Y⊆X.
Proper Subset
The term proper subset can be defined as subset of but not equal to. A Set X is a proper subset of set Y (Written as X ⊂ Y) if every element of X is an element of set Y and |X| < |Y|.
Example − Let, X = {1,2,3,4,5,6} and Y = {1,2}. Here set Y ⊂ X, since all elements in Y are contained in X too and X has at least one element which is more than set Y.
Universal Set
It is a collection of all elements in a particular context or application. All the sets in that context or application are essentially subsets of this universal set. Universal sets are represented as U.
Example − We may define U as the set of all animals on earth. In this case, a set of all mammals is a subset of U, a set of all fishes is a subset of U, a set of all insects is a subset of U, and so on.
Empty Set or Null Set
An empty set contains no elements. It is denoted by Φ. As the number of elements in an empty set is finite, empty set is a finite set. The cardinality of empty set or null set is zero.
Example S = {x|x ∈ N and 7 < x < 8} = Φ
Singleton Set or Unit Set
A Singleton set or Unit set contains only one element. A singleton set is denoted by {s}.
Example − S = {x|x ∈ N, 7 < x < 9} = {8}
Equal Set
If two sets contain the same elements, they are said to be equal.
Example − If A = {1,2,6} and B = {6,1,2}, they are equal as every element of set A is an element of set B and every element of set B is an element of set A.
Equivalent Set
If the cardinalities of two sets are same, they are called equivalent sets.
Example − If A = {1,2,6} and B = {16,17,22}, they are equivalent as cardinality of A is equal to the cardinality of B. i.e. |A| = |B| = 3
Overlapping Set
Two sets that have at least one common element are called overlapping sets. In case of overlapping sets −
$$n\left ( A\cup B \right ) = n\left ( A \right ) + n\left ( B \right ) - n\left ( A\cap B \right )$$
$$n\left ( A\cup B \right ) = n\left ( A-B \right )+n\left ( B-A \right )+n\left ( A\cap B \right )$$
$$n\left ( A \right ) = n\left ( A-B \right )+n\left ( A\cap B \right )$$
$$n\left ( B \right ) = n\left ( B-A \right )+n\left ( A\cap B \right )$$
Example − Let, A = {1,2,6} and B = {6,12,42}. There is a common element 6, hence these sets are overlapping sets.
Disjoint Set
Two sets A and B are called disjoint sets if they do not have even one element in common. Therefore, disjoint sets have the following properties −
$$n\left ( A\cap B \right ) = \phi$$
$$n\left ( A\cup B \right ) = n\left ( A \right )+n\left ( B \right )$$
Example − Let, A = {1,2,6} and B = {7,9,14}, there is not a single common element, hence these sets are overlapping sets.
Operations on Classical Sets
Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product.
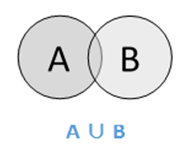
Union
The union of sets A and B (denoted by A ∪ BA ∪ B) is the set of elements which are in A, in B, or in both A and B. Hence, A ∪ B = {x|x ∈ A OR x ∈ B}.
Example − If A = {10,11,12,13} and B = {13,14,15}, then A ∪ B = {10,11,12,13,14,15} The common element occurs only once.
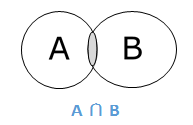
Intersection
The intersection of sets A and B (denoted by A ∩ B) is the set of elements which are in both A and B. Hence, A ∩ B = {x|x ∈ A AND x ∈ B}.
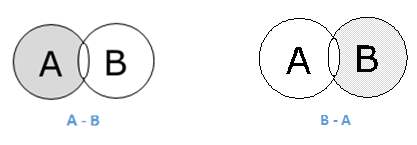
Difference/ Relative Complement
The set difference of sets A and B (denoted by AB) is the set of elements which are only in A but not in B. Hence, A B = {x|x ∈ A AND x ∉ B}.
Example − If A = {10,11,12,13} and B = {13,14,15}, then (A B) = {10,11,12} and (B A) = {14,15}. Here, we can see (A B) ≠ (B A)
Complement of a Set
The complement of a set A (denoted by A) is the set of elements which are not in set A. Hence, A′ = {x|x ∉ A}.
More specifically, A′ = (UA) where U is a universal set which contains all objects.
Example − If A = {x|x belongs to set of add integers} then A′ = {y|y does not belong to set of odd integers}
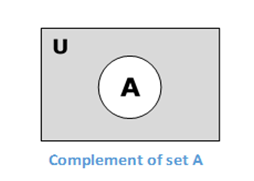
Cartesian Product / Cross Product
The Cartesian product of n number of sets A1,A2,An denoted as A1 × A2...× An can be defined as all possible ordered pairs (x1,x2,xn) where x1 ∈ A1,x2 ∈ A2,xn ∈ An
Example − If we take two sets A = {a,b} and B = {1,2},
The Cartesian product of A and B is written as A × B = {(a,1),(a,2),(b,1),(b,2)}
And, the Cartesian product of B and A is written as B × A = {(1,a),(1,b),(2,a),(2,b)}
Properties of Classical Sets
Properties on sets play an important role for obtaining the solution. Following are the different properties of classical sets −
Commutative Property
Having two sets A and B, this property states −
$$A \cup B = B \cup A$$
$$A \cap B = B \cap A$$
Associative Property
Having three sets A, B and C, this property states −
$$A\cup \left ( B\cup C \right ) = \left ( A\cup B \right )\cup C$$
$$A\cap \left ( B\cap C \right ) = \left ( A\cap B \right )\cap C$$
Distributive Property
Having three sets A, B and C, this property states −
$$A\cup \left ( B\cap C \right ) = \left ( A\cup B \right )\cap \left ( A\cup C \right )$$
$$A\cap \left ( B\cup C \right ) = \left ( A\cap B \right )\cup \left ( A\cap C \right )$$
Idempotency Property
For any set A, this property states −
$$A\cup A = A$$
$$A\cap A = A$$
Identity Property
For set A and universal set X, this property states −
$$A\cup \varphi = A$$
$$A\cap X = A$$
$$A\cap \varphi = \varphi$$
$$A\cup X = X$$
Transitive Property
Having three sets A, B and C, the property states −
If $A\subseteq B\subseteq C$, then $A\subseteq C$
Involution Property
For any set A, this property states −
$$\overline{{\overline{A}}} = A$$
De Morgans Law
It is a very important law and supports in proving tautologies and contradiction. This law states −
$$\overline{A\cap B} = \overline{A} \cup \overline{B}$$
$$\overline{A\cup B} = \overline{A} \cap \overline{B}$$
Fuzzy Logic - Set Theory
Fuzzy sets can be considered as an extension and gross oversimplification of classical sets. It can be best understood in the context of set membership. Basically it allows partial membership which means that it contain elements that have varying degrees of membership in the set. From this, we can understand the difference between classical set and fuzzy set. Classical set contains elements that satisfy precise properties of membership while fuzzy set contains elements that satisfy imprecise properties of membership.
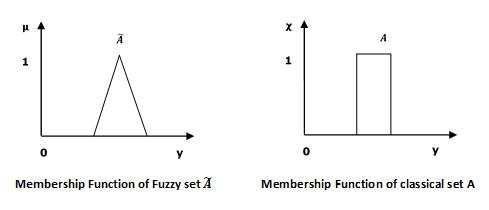
Mathematical Concept
A fuzzy set $\widetilde{A}$ in the universe of information $U$ can be defined as a set of ordered pairs and it can be represented mathematically as −
$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$
Here $\mu _{\widetilde{A}}\left ( y \right )$ = degree of membership of $y$ in \widetilde{A}, assumes values in the range from 0 to 1, i.e., $\mu _{\widetilde{A}}(y)\in \left [ 0,1 \right ]$.
Representation of fuzzy set
Let us now consider two cases of universe of information and understand how a fuzzy set can be represented.
Case 1
When universe of information $U$ is discrete and finite −
$$\widetilde{A} = \left \{ \frac{\mu _{\widetilde{A}}\left ( y_1 \right )}{y_1} +\frac{\mu _{\widetilde{A}}\left ( y_2 \right )}{y_2} +\frac{\mu _{\widetilde{A}}\left ( y_3 \right )}{y_3} +...\right \}$$
$= \left \{ \sum_{i=1}^{n}\frac{\mu _{\widetilde{A}}\left ( y_i \right )}{y_i} \right \}$
Case 2
When universe of information $U$ is continuous and infinite −
$$\widetilde{A} = \left \{ \int \frac{\mu _{\widetilde{A}}\left ( y \right )}{y} \right \}$$
In the above representation, the summation symbol represents the collection of each element.
Operations on Fuzzy Sets
Having two fuzzy sets $\widetilde{A}$ and $\widetilde{B}$, the universe of information $U$ and an element of the universe, the following relations express the union, intersection and complement operation on fuzzy sets.
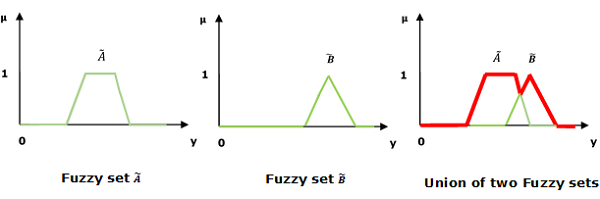
Union/Fuzzy OR
Let us consider the following representation to understand how the Union/Fuzzy OR relation works −
$$\mu _{{\widetilde{A}\cup \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\vee \mu _\widetilde{B} \quad \forall y \in U$$
Here ∨ represents the max operation.
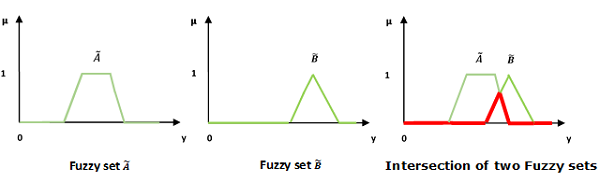
Intersection/Fuzzy AND
Let us consider the following representation to understand how the Intersection/Fuzzy AND relation works −
$$\mu _{{\widetilde{A}\cap \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\wedge \mu _\widetilde{B} \quad \forall y \in U$$
Here ∧ represents the min operation.
Complement/Fuzzy NOT
Let us consider the following representation to understand how the Complement/Fuzzy NOT relation works −
$$\mu _{\widetilde{A}} = 1-\mu _{\widetilde{A}}\left ( y \right )\quad y \in U$$
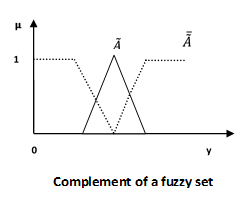
Properties of Fuzzy Sets
Let us discuss the different properties of fuzzy sets.
Commutative Property
Having two fuzzy sets $\widetilde{A}$ and $\widetilde{B}$, this property states −
$$\widetilde{A}\cup \widetilde{B} = \widetilde{B}\cup \widetilde{A}$$
$$\widetilde{A}\cap \widetilde{B} = \widetilde{B}\cap \widetilde{A}$$
Associative Property
Having three fuzzy sets $\widetilde{A}$, $\widetilde{B}$ and $\widetilde{C}$, this property states −
$$(\widetilde{A}\cup \left \widetilde{B}) \cup \widetilde{C} \right = \left \widetilde{A} \cup (\widetilde{B}\right )\cup \widetilde{C})$$
$$(\widetilde{A}\cap \left \widetilde{B}) \cap \widetilde{C} \right = \left \widetilde{A} \cup (\widetilde{B}\right \cap \widetilde{C})$$
Distributive Property
Having three fuzzy sets $\widetilde{A}$, $\widetilde{B}$ and $\widetilde{C}$, this property states −
$$\widetilde{A}\cup \left ( \widetilde{B} \cap \widetilde{C}\right ) = \left ( \widetilde{A} \cup \widetilde{B}\right )\cap \left ( \widetilde{A}\cup \widetilde{C} \right )$$
$$\widetilde{A}\cap \left ( \widetilde{B}\cup \widetilde{C} \right ) = \left ( \widetilde{A} \cap \widetilde{B} \right )\cup \left ( \widetilde{A}\cap \widetilde{C} \right )$$
Idempotency Property
For any fuzzy set $\widetilde{A}$, this property states −
$$\widetilde{A}\cup \widetilde{A} = \widetilde{A}$$
$$\widetilde{A}\cap \widetilde{A} = \widetilde{A}$$
Identity Property
For fuzzy set $\widetilde{A}$ and universal set $U$, this property states −
$$\widetilde{A}\cup \varphi = \widetilde{A}$$
$$\widetilde{A}\cap U = \widetilde{A}$$
$$\widetilde{A}\cap \varphi = \varphi$$
$$\widetilde{A}\cup U = U$$
Transitive Property
Having three fuzzy sets $\widetilde{A}$, $\widetilde{B}$ and $\widetilde{C}$, this property states −
$$If \: \widetilde{A}\subseteq \widetilde{B}\subseteq \widetilde{C},\:then\:\widetilde{A}\subseteq \widetilde{C}$$
Involution Property
For any fuzzy set $\widetilde{A}$, this property states −
$$\overline{\overline{\widetilde{A}}} = \widetilde{A}$$
De Morgans Law
This law plays a crucial role in proving tautologies and contradiction. This law states −
$$\overline{{\widetilde{A}\cap \widetilde{B}}} = \overline{\widetilde{A}}\cup \overline{\widetilde{B}}$$
$$\overline{{\widetilde{A}\cup \widetilde{B}}} = \overline{\widetilde{A}}\cap \overline{\widetilde{B}}$$
Fuzzy Logic - Membership Function
We already know that fuzzy logic is not logic that is fuzzy but logic that is used to describe fuzziness. This fuzziness is best characterized by its membership function. In other words, we can say that membership function represents the degree of truth in fuzzy logic.
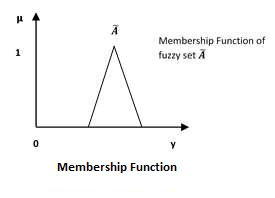
Following are a few important points relating to the membership function −
Membership functions were first introduced in 1965 by Lofti A. Zadeh in his first research paper fuzzy sets.
Membership functions characterize fuzziness (i.e., all the information in fuzzy set), whether the elements in fuzzy sets are discrete or continuous.
Membership functions can be defined as a technique to solve practical problems by experience rather than knowledge.
Membership functions are represented by graphical forms.
Rules for defining fuzziness are fuzzy too.
Mathematical Notation
We have already studied that a fuzzy set à in the universe of information U can be defined as a set of ordered pairs and it can be represented mathematically as −
$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$
Here $\mu \widetilde{A}\left (\bullet \right )$ = membership function of $\widetilde{A}$; this assumes values in the range from 0 to 1, i.e., $\mu \widetilde{A}\left (\bullet \right )\in \left [ 0,1 \right ]$. The membership function $\mu \widetilde{A}\left (\bullet \right )$ maps $U$ to the membership space$M$.
The dot $\left (\bullet \right )$ in the membership function described above, represents the element in a fuzzy set; whether it is discrete or continuous.
Features of Membership Functions
We will now discuss the different features of Membership Functions.
Core
For any fuzzy set $\widetilde{A}$, the core of a membership function is that region of universe that is characterize by full membership in the set. Hence, core consists of all those elements $y$ of the universe of information such that,
$$\mu _{\widetilde{A}}\left ( y \right ) = 1$$
Support
For any fuzzy set $\widetilde{A}$, the support of a membership function is the region of universe that is characterize by a nonzero membership in the set. Hence core consists of all those elements $y$ of the universe of information such that,
$$\mu _{\widetilde{A}}\left ( y \right ) > 0$$
Boundary
For any fuzzy set $\widetilde{A}$, the boundary of a membership function is the region of universe that is characterized by a nonzero but incomplete membership in the set. Hence, core consists of all those elements $y$ of the universe of information such that,
$$1 > \mu _{\widetilde{A}}\left ( y \right ) > 0$$
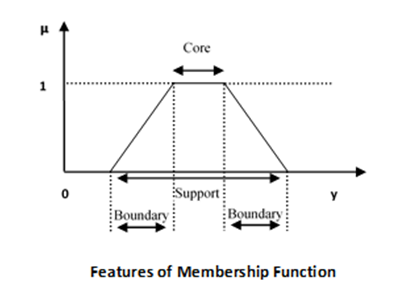
Fuzzification
It may be defined as the process of transforming a crisp set to a fuzzy set or a fuzzy set to fuzzier set. Basically, this operation translates accurate crisp input values into linguistic variables.
Following are the two important methods of fuzzification −
Support Fuzzification(s-fuzzification) Method
In this method, the fuzzified set can be expressed with the help of the following relation −
$$\widetilde{A} = \mu _1Q\left ( x_1 \right )+\mu _2Q\left ( x_2 \right )+...+\mu _nQ\left ( x_n \right )$$
Here the fuzzy set $Q\left ( x_i \right )$ is called as kernel of fuzzification. This method is implemented by keeping $\mu _i$ constant and $x_i$ being transformed to a fuzzy set $Q\left ( x_i \right )$.
Grade Fuzzification (g-fuzzification) Method
It is quite similar to the above method but the main difference is that it kept $x_i$ constant and $\mu _i$ is expressed as a fuzzy set.
Defuzzification
It may be defined as the process of reducing a fuzzy set into a crisp set or to convert a fuzzy member into a crisp member.
We have already studied that the fuzzification process involves conversion from crisp quantities to fuzzy quantities. In a number of engineering applications, it is necessary to defuzzify the result or rather fuzzy result so that it must be converted to crisp result. Mathematically, the process of Defuzzification is also called rounding it off.
The different methods of Defuzzification are described below −
Max-Membership Method
This method is limited to peak output functions and also known as height method. Mathematically it can be represented as follows −
$$\mu _{\widetilde{A}}\left ( x^* \right )>\mu _{\widetilde{A}}\left ( x \right ) \: for \:all\:x \in X$$
Here, $x^*$ is the defuzzified output.
Centroid Method
This method is also known as the center of area or the center of gravity method. Mathematically, the defuzzified output $x^*$ will be represented as −
$$x^* = \frac{\int \mu _{\widetilde{A}}\left ( x \right ).xdx}{\int \mu _{\widetilde{A}}\left ( x \right ).dx}$$
Weighted Average Method
In this method, each membership function is weighted by its maximum membership value. Mathematically, the defuzzified output $x^*$ will be represented as −
$$x^* = \frac{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right ).\overline{x_i}}{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right )}$$
Mean-Max Membership
This method is also known as the middle of the maxima. Mathematically, the defuzzified output $x^*$ will be represented as −
$$x^* = \frac{\displaystyle \sum_{i=1}^{n}\overline{x_i}}{n}$$
Fuzzy Logic - Traditional Fuzzy Refresher
Logic, which was originally just the study of what distinguishes sound argument from unsound argument, has now developed into a powerful and rigorous system whereby true statements can be discovered, given other statements that are already known to be true.
Predicate Logic
This logic deals with predicates, which are propositions containing variables.
A predicate is an expression of one or more variables defined on some specific domain. A predicate with variables can be made a proposition by either assigning a value to the variable or by quantifying the variable.
Following are a few examples of predicates −
- Let E(x, y) denote "x = y"
- Let X(a, b, c) denote "a + b + c = 0"
- Let M(x, y) denote "x is married to y"
Propositional Logic
A proposition is a collection of declarative statements that have either a truth value "true or a truth value "false". A propositional consists of propositional variables and connectives. The propositional variables are dented by capital letters (A, B, etc). The connectives connect the propositional variables.
A few examples of Propositions are given below −
- "Man is Mortal", it returns truth value TRUE
- "12 + 9 = 3 2", it returns truth value FALSE
The following is not a Proposition −
"A is less than 2" − It is because unless we give a specific value of A, we cannot say whether the statement is true or false.
Connectives
In propositional logic, we use the following five connectives −
- OR (∨∨)
- AND (∧∧)
- Negation/ NOT (¬¬)
- Implication / if-then (→→)
- If and only if (⇔⇔)
OR (∨∨)
The OR operation of two propositions A and B (written as ABAB) is true if at least any of the propositional variable A or B is true.
The truth table is as follows −
| A | B | A ∨ B |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
AND (∧∧)
The AND operation of two propositions A and B (written as ABAB) is true if both the propositional variable A and B is true.
The truth table is as follows −
| A | B | A ∧ B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
Negation (¬¬)
The negation of a proposition A (written as ¬A¬A) is false when A is true and is true when A is false.
The truth table is as follows −
| A | ¬A |
|---|---|
| True | False |
| False | True |
Implication / if-then (→→)
An implication A→BA→B is the proposition if A, then B. It is false if A is true and B is false. The rest cases are true.
The truth table is as follows −
| A | B | A→B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | True |
| False | False | True |
If and only if (⇔⇔)
A⇔BA⇔B is a bi-conditional logical connective which is true when p and q are same, i.e., both are false or both are true.
The truth table is as follows −
| A | B | A⇔B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | True |
Well Formed Formula
Well Formed Formula (wff) is a predicate holding one of the following −
- All propositional constants and propositional variables are wffs.
- If x is a variable and Y is a wff, ∀xY and ∃xY are also wff.
- Truth value and false values are wffs.
- Each atomic formula is a wff.
- All connectives connecting wffs are wffs.
Quantifiers
The variable of predicates is quantified by quantifiers. There are two types of quantifier in predicate logic −
- Universal Quantifier
- Existential Quantifier
Universal Quantifier
Universal quantifier states that the statements within its scope are true for every value of the specific variable. It is denoted by the symbol ∀.
∀xP(x) is read as for every value of x, P(x) is true.
Example − "Man is mortal" can be transformed into the propositional form ∀xP(x). Here, P(x) is the predicate which denotes that x is mortal and the universe of discourse is all men.
Existential Quantifier
Existential quantifier states that the statements within its scope are true for some values of the specific variable. It is denoted by the symbol ∃.
∃xP(x) for some values of x is read as, P(x) is true.
Example − "Some people are dishonest" can be transformed into the propositional form ∃x P(x) where P(x) is the predicate which denotes x is dishonest and the universe of discourse is some people.
Nested Quantifiers
If we use a quantifier that appears within the scope of another quantifier, it is called a nested quantifier.
Example
- ∀ a∃bP(x,y) where P(a,b) denotes a+b = 0
- ∀ a∀b∀cP(a,b,c) where P(a,b) denotes a+(b+c) = (a+b)+c
Note − ∀a∃bP(x,y) ≠ ∃a∀bP(x,y)
Fuzzy Logic - Approximate Reasoning
Following are the different modes of approximate reasoning −
Categorical Reasoning
In this mode of approximate reasoning, the antecedents, containing no fuzzy quantifiers and fuzzy probabilities, are assumed to be in canonical form.
Qualitative Reasoning
In this mode of approximate reasoning, the antecedents and consequents have fuzzy linguistic variables; the input-output relationship of a system is expressed as a collection of fuzzy IF-THEN rules. This reasoning is mainly used in control system analysis.
Syllogistic Reasoning
In this mode of approximation reasoning, antecedents with fuzzy quantifiers are related to inference rules. This is expressed as −
x = S1A′s are B′s
y = S2C′s are D′s
------------------------
z = S3E′s are F′s
Here A,B,C,D,E,F are fuzzy predicates.
S1 and S2 are given fuzzy quantifiers.
S3 is the fuzzy quantifier which has to be decided.
Dispositional Reasoning
In this mode of approximation reasoning, the antecedents are dispositions that may contain the fuzzy quantifier usually. The quantifier Usually links together the dispositional and syllogistic reasoning; hence it pays an important role.
For example, the projection rule of inference in dispositional reasoning can be given as follows −
usually( (L,M) is R ) ⇒ usually (L is [R ↓ L])
Here [R ↓ L] is the projection of fuzzy relation R on L
Fuzzy Logic Rule Base
It is a known fact that a human being is always comfortable making conversations in natural language. The representation of human knowledge can be done with the help of following natural language expression −
IF antecedent THEN consequent
The expression as stated above is referred to as the Fuzzy IF-THEN rule base.
Canonical Form
Following is the canonical form of Fuzzy Logic Rule Base −
Rule 1 − If condition C1, then restriction R1
Rule 2 − If condition C1, then restriction R2
.
.
.
Rule n − If condition C1, then restriction Rn
Interpretations of Fuzzy IF-THEN Rules
Fuzzy IF-THEN Rules can be interpreted in the following four forms −
Assignment Statements
These kinds of statements use = (equal to sign) for the purpose of assignment. They are of the following form −
a = hello
climate = summer
Conditional Statements
These kinds of statements use the IF-THEN rule base form for the purpose of condition. They are of the following form −
IF temperature is high THEN Climate is hot
IF food is fresh THEN eat.
Unconditional Statements
They are of the following form −
GOTO 10
turn the Fan off
Linguistic Variable
We have studied that fuzzy logic uses linguistic variables which are the words or sentences in a natural language. For example, if we say temperature, it is a linguistic variable; the values of which are very hot or cold, slightly hot or cold, very warm, slightly warm, etc. The words very, slightly are the linguistic hedges.
Characterization of Linguistic Variable
Following four terms characterize the linguistic variable −
- Name of the variable, generally represented by x.
- Term set of the variable, generally represented by t(x).
- Syntactic rules for generating the values of the variable x.
- Semantic rules for linking every value of x and its significance.
Propositions in Fuzzy Logic
As we know that propositions are sentences expressed in any language which are generally expressed in the following canonical form −
s as P
Here, s is the Subject and P is Predicate.
For example, Delhi is the capital of India, this is a proposition where Delhi is the subject and is the capital of India is the predicate which shows the property of subject.
We know that logic is the basis of reasoning and fuzzy logic extends the capability of reasoning by using fuzzy predicates, fuzzy-predicate modifiers, fuzzy quantifiers and fuzzy qualifiers in fuzzy propositions which creates the difference from classical logic.
Propositions in fuzzy logic include the following −
Fuzzy Predicate
Almost every predicate in natural language is fuzzy in nature hence, fuzzy logic has the predicates like tall, short, warm, hot, fast, etc.
Fuzzy-predicate Modifiers
We discussed linguistic hedges above; we also have many fuzzy-predicate modifiers which act as hedges. They are very essential for producing the values of a linguistic variable. For example, the words very, slightly are modifiers and the propositions can be like water is slightly hot.
Fuzzy Quantifiers
It can be defined as a fuzzy number which gives a vague classification of the cardinality of one or more fuzzy or non-fuzzy sets. It can be used to influence probability within fuzzy logic. For example, the words many, most, frequently are used as fuzzy quantifiers and the propositions can be like most people are allergic to it.
Fuzzy Qualifiers
Let us now understand Fuzzy Qualifiers. A Fuzzy Qualifier is also a proposition of Fuzzy Logic. Fuzzy qualification has the following forms −
Fuzzy Qualification Based on Truth
It claims the degree of truth of a fuzzy proposition.
Expression − It is expressed as x is t. Here, t is a fuzzy truth value.
Example − (Car is black) is NOT VERY True.
Fuzzy Qualification Based on Probability
It claims the probability, either numerical or an interval, of fuzzy proposition.
Expression − It is expressed as x is λ. Here, λ is a fuzzy probability.
Example − (Car is black) is Likely.
Fuzzy Qualification Based on Possibility
It claims the possibility of fuzzy proposition.
Expression − It is expressed as x is π. Here, π is a fuzzy possibility.
Example − (Car is black) is Almost Impossible.
Fuzzy Logic - Inference System
Fuzzy Inference System is the key unit of a fuzzy logic system having decision making as its primary work. It uses the IFTHEN rules along with connectors OR or AND for drawing essential decision rules.
Characteristics of Fuzzy Inference System
Following are some characteristics of FIS −
The output from FIS is always a fuzzy set irrespective of its input which can be fuzzy or crisp.
It is necessary to have fuzzy output when it is used as a controller.
A defuzzification unit would be there with FIS to convert fuzzy variables into crisp variables.
Functional Blocks of FIS
The following five functional blocks will help you understand the construction of FIS −
Rule Base − It contains fuzzy IF-THEN rules.
Database − It defines the membership functions of fuzzy sets used in fuzzy rules.
Decision-making Unit − It performs operation on rules.
Fuzzification Interface Unit − It converts the crisp quantities into fuzzy quantities.
Defuzzification Interface Unit − It converts the fuzzy quantities into crisp quantities. Following is a block diagram of fuzzy interference system.
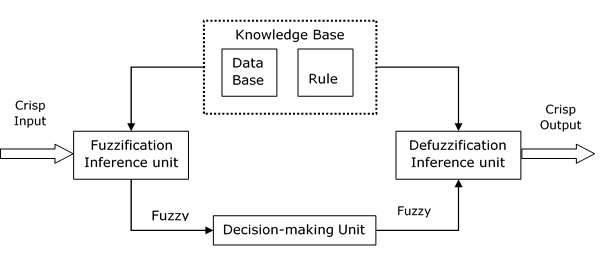
Working of FIS
The working of the FIS consists of the following steps −
A fuzzification unit supports the application of numerous fuzzification methods, and converts the crisp input into fuzzy input.
A knowledge base - collection of rule base and database is formed upon the conversion of crisp input into fuzzy input.
The defuzzification unit fuzzy input is finally converted into crisp output.
Methods of FIS
Let us now discuss the different methods of FIS. Following are the two important methods of FIS, having different consequent of fuzzy rules −
- Mamdani Fuzzy Inference System
- Takagi-Sugeno Fuzzy Model (TS Method)
Mamdani Fuzzy Inference System
This system was proposed in 1975 by Ebhasim Mamdani. Basically, it was anticipated to control a steam engine and boiler combination by synthesizing a set of fuzzy rules obtained from people working on the system.
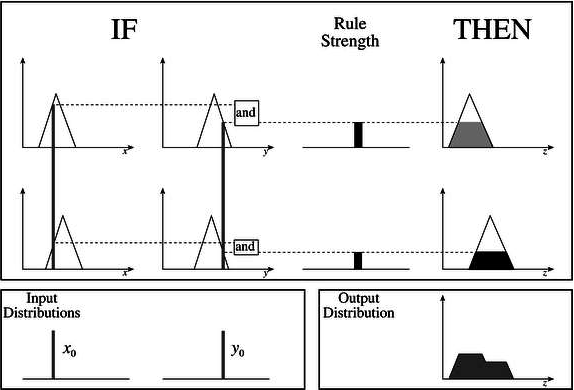
Steps for Computing the Output
Following steps need to be followed to compute the output from this FIS −
Step 1 − Set of fuzzy rules need to be determined in this step.
Step 2 − In this step, by using input membership function, the input would be made fuzzy.
Step 3 − Now establish the rule strength by combining the fuzzified inputs according to fuzzy rules.
Step 4 − In this step, determine the consequent of rule by combining the rule strength and the output membership function.
Step 5 − For getting output distribution combine all the consequents.
Step 6 − Finally, a defuzzified output distribution is obtained.
Following is a block diagram of Mamdani Fuzzy Interface System.
Takagi-Sugeno Fuzzy Model (TS Method)
This model was proposed by Takagi, Sugeno and Kang in 1985. Format of this rule is given as −
IF x is A and y is B THEN Z = f(x,y)
Here, AB are fuzzy sets in antecedents and z = f(x,y) is a crisp function in the consequent.
Fuzzy Inference Process
The fuzzy inference process under Takagi-Sugeno Fuzzy Model (TS Method) works in the following way −
Step 1: Fuzzifying the inputs − Here, the inputs of the system are made fuzzy.
Step 2: Applying the fuzzy operator − In this step, the fuzzy operators must be applied to get the output.
Rule Format of the Sugeno Form
The rule format of Sugeno form is given by −
if 7 = x and 9 = y then output is z = ax+by+c
Comparison between the two methods
Let us now understand the comparison between the Mamdani System and the Sugeno Model.
Output Membership Function − The main difference between them is on the basis of output membership function. The Sugeno output membership functions are either linear or constant.
Aggregation and Defuzzification Procedure − The difference between them also lies in the consequence of fuzzy rules and due to the same their aggregation and defuzzification procedure also differs.
Mathematical Rules − More mathematical rules exist for the Sugeno rule than the Mamdani rule.
Adjustable Parameters − The Sugeno controller has more adjustable parameters than the Mamdani controller.
Fuzzy Logic - Database and Queries
We have studied in our previous chapters that Fuzzy Logic is an approach to computing based on "degrees of truth" rather than the usual "true or false" logic. It deals with reasoning that is approximate rather than precise to solve problems in a way that more resembles human logic, hence database querying process by the two valued realization of Boolean algebra is not adequate.
Fuzzy Scenario of Relations on Databases
The Fuzzy Scenario of Relations on Databases can be understood with the help of the following example −
Example
Suppose we have a database having the records of persons who visited India. In simple database, we will have the entries made in the following way −
| Name | Age | Citizen | Visited Country | Days Spent | Year of Visit |
|---|---|---|---|---|---|
| John Smith | 35 | U.S. | India | 41 | 1999 |
| John Smith | 35 | U.S. | Italy | 72 | 1999 |
| John Smith | 35 | U.S. | Japan | 31 | 1999 |
Now, if anyone queries about the person who visited India and Japan in the year 99 and is the citizen of US, then the output will show two entries having the name of John Smith. This is simple query generating simple output.
But what if we want to know whether the person in the above query is young or not. According to the above result, the age of the person is 35 years. But can we assume the person to be young or not? Similarly, same thing can be applied on the other fields like days spent, year of visit, etc.
The solution of the above issues can be found with the help of Fuzzy Value sets as follows −
FV(Age){ very young, young, somewhat old, old }
FV(Days Spent){ barely few days, few days, quite a few days, many days }
FV(Year of Visit){distant past, recent past, recent }
Now if any query will have the fuzzy value then the result will also be fuzzy in nature.
Fuzzy Query System
A fuzzy query system is an interface to users to get information from the database using (quasi) natural language sentences. Many fuzzy query implementations have been proposed, resulting in slightly different languages. Although there are some variations according to the particularities of different implementations, the answer to a fuzzy query sentence is generally a list of records, ranked by the degree of matching.
Fuzzy Logic - Quantification
In modeling natural language statements, quantified statements play an important role. It means that NL heavily depends on quantifying construction which often includes fuzzy concepts like almost all, many, etc. Following are a few examples of quantifying propositions −
- Every student passed the exam.
- Every sport car is expensive.
- Many students passed the exam.
- Many sports cars are expensive.
In the above examples, the quantifiers Every and Many are applied to the crisp restrictions students as well as crisp scope (person who)passed the exam and cars as well as crisp scope sports.
Fuzzy Events, Fuzzy Means and Fuzzy Variances
With the help of an example, we can understand the above concepts. Let us assume that we are a shareholder of a company named ABC. And at present the company is selling each of its share for ₹40. There are three different companies whose business is similar to ABC but these are offering their shares at different rates - ₹100 a share, ₹85 a share and ₹60 a share respectively.
Now the probability distribution of this price takeover is as follows −
| Price | ₹100 | ₹85 | ₹60 |
|---|---|---|---|
| Probability | 0.3 | 0.5 | 0.2 |
Now, from the standard probability theory, the above distribution gives a mean of expected price as below −
$100 0.3 + 85 0.5 + 60 0.2 = 84.5$
And, from the standard probability theory, the above distribution gives a variance of expected price as below −
$(100 84.5)2 0.3 + (85 84.5)2 0.5 + (60 84.5)2 0.2 = 124.825$
Suppose the degree of membership of 100 in this set is 0.7, that of 85 is 1, and the degree of membership is 0.5 for the value 60. These can be reflected in the following fuzzy set −
$$\left \{ \frac{0.7}{100}, \: \frac{1}{85}, \: \frac{0.5}{60}, \right \}$$
The fuzzy set obtained in this manner is called a fuzzy event.
We want the probability of the fuzzy event for which our calculation gives −
$0.7 0.3 + 1 0.5 + 0.5 0.2 = 0.21 + 0.5 + 0.1 = 0.81$
Now, we need to calculate the fuzzy mean and the fuzzy variance, the calculation is as follows −
Fuzzy_mean $= \left ( \frac{1}{0.81} \right ) (100 0.7 0.3 + 85 1 0.5 + 60 0.5 0.2)$
$= 85.8$
Fuzzy_Variance $= 7496.91 7361.91 = 135.27$
Fuzzy Logic - Decision Making
It is an activity which includes the steps to be taken for choosing a suitable alternative from those that are needed for realizing a certain goal.
Steps for Decision Making
Let us now discuss the steps involved in the decision making process −
Determining the Set of Alternatives − In this step, the alternatives from which the decision has to be taken must be determined.
Evaluating Alternative − Here, the alternatives must be evaluated so that the decision can be taken about one of the alternatives.
Comparison between Alternatives − In this step, a comparison between the evaluated alternatives is done.
Types of Decision
Making We will now understand the different types of decision making.
Individual Decision Making
In this type of decision making, only a single person is responsible for taking decisions. The decision making model in this kind can be characterized as −
Set of possible actions
Set of goals $G_i\left ( i \: \in \: X_n \right );$
Set of Constraints $C_j\left ( j \: \in \: X_m \right )$
The goals and constraints stated above are expressed in terms of fuzzy sets.
Now consider a set A. Then, the goal and constraints for this set are given by −
$G_i\left ( a \right )$ = composition$\left [ G_i\left ( a \right ) \right ]$ = $G_i^1\left ( G_i\left ( a \right ) \right )$ with $G_i^1$
$C_j\left ( a \right )$ = composition$\left [ C_j\left ( a \right ) \right ]$ = $C_j^1\left ( C_j\left ( a \right ) \right )$ with $C_j^1$ for $a\:\in \:A$
The fuzzy decision in the above case is given by −
$$F_D = min[i\in X_{n}^{in}fG_i\left ( a \right ),j\in X_{m}^{in}fC_j\left ( a \right )]$$
Multi-person Decision Making
Decision making in this case includes several persons so that the expert knowledge from various persons is utilized to make decisions.
Calculation for this can be given as follows −
Number of persons preferring $x_i$ to $x_j$ = $N\left ( x_i, \: x_j \right )$
Total number of decision makers = $n$
Then, $SC\left ( x_i, \: x_j \right ) = \frac{N\left ( x_i, \: x_j \right )}{n}$
Multi-objective Decision Making
Multi-objective decision making occurs when there are several objectives to be realized. There are following two issues in this type of decision making −
To acquire proper information related to the satisfaction of the objectives by various alternatives.
To weigh the relative importance of each objective.
Mathematically we can define a universe of n alternatives as −
$A = \left [ a_1, \:a_2,\:..., \: a_i, \: ..., \:a_n \right ]$
And the set of m objectives as $O = \left [ o_1, \:o_2,\:..., \: o_i, \: ..., \:o_n \right ]$
Multi-attribute Decision Making
Multi-attribute decision making takes place when the evaluation of alternatives can be carried out based on several attributes of the object. The attributes can be numerical data, linguistic data and qualitative data.
Mathematically, the multi-attribute evaluation is carried out on the basis of linear equation as follows −
$$Y = A_1X_1+A_2X_2+...+A_iX_i+...+A_rX_r$$
Fuzzy Logic - Control System
Fuzzy logic is applied with great success in various control application. Almost all the consumer products have fuzzy control. Some of the examples include controlling your room temperature with the help of air-conditioner, anti-braking system used in vehicles, control on traffic lights, washing machines, large economic systems, etc.
Why Use Fuzzy Logic in Control Systems
A control system is an arrangement of physical components designed to alter another physical system so that this system exhibits certain desired characteristics. Following are some reasons of using Fuzzy Logic in Control Systems −
While applying traditional control, one needs to know about the model and the objective function formulated in precise terms. This makes it very difficult to apply in many cases.
By applying fuzzy logic for control we can utilize the human expertise and experience for designing a controller.
The fuzzy control rules, basically the IF-THEN rules, can be best utilized in designing a controller.
Assumptions in Fuzzy Logic Control (FLC) Design
While designing fuzzy control system, the following six basic assumptions should be made −
The plant is observable and controllable − It must be assumed that the input, output as well as state variables are available for observation and controlling purpose.
Existence of a knowledge body − It must be assumed that there exist a knowledge body having linguistic rules and a set of input-output data set from which rules can be extracted.
Existence of solution − It must be assumed that there exists a solution.
Good enough solution is enough − The control engineering must look for good enough solution rather than an optimum one.
Range of precision − Fuzzy logic controller must be designed within an acceptable range of precision.
Issues regarding stability and optimality − The issues of stability and optimality must be open in designing Fuzzy logic controller rather than addressed explicitly.
Architecture of Fuzzy Logic Control
The following diagram shows the architecture of Fuzzy Logic Control (FLC).
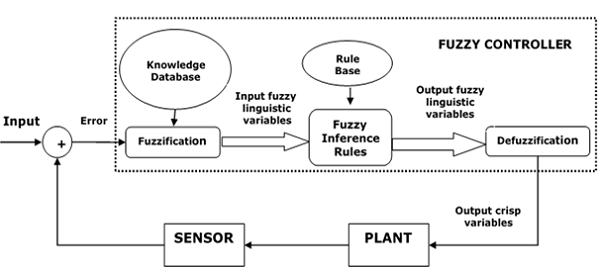
Major Components of FLC
Followings are the major components of the FLC as shown in the above figure −
Fuzzifier − The role of fuzzifier is to convert the crisp input values into fuzzy values.
Fuzzy Knowledge Base − It stores the knowledge about all the input-output fuzzy relationships. It also has the membership function which defines the input variables to the fuzzy rule base and the output variables to the plant under control.
Fuzzy Rule Base − It stores the knowledge about the operation of the process of domain.
Inference Engine − It acts as a kernel of any FLC. Basically it simulates human decisions by performing approximate reasoning.
Defuzzifier − The role of defuzzifier is to convert the fuzzy values into crisp values getting from fuzzy inference engine.
Steps in Designing FLC
Following are the steps involved in designing FLC −
Identification of variables − Here, the input, output and state variables must be identified of the plant which is under consideration.
Fuzzy subset configuration − The universe of information is divided into number of fuzzy subsets and each subset is assigned a linguistic label. Always make sure that these fuzzy subsets include all the elements of universe.
Obtaining membership function − Now obtain the membership function for each fuzzy subset that we get in the above step.
Fuzzy rule base configuration − Now formulate the fuzzy rule base by assigning relationship between fuzzy input and output.
Fuzzification − The fuzzification process is initiated in this step.
Combining fuzzy outputs − By applying fuzzy approximate reasoning, locate the fuzzy output and merge them.
Defuzzification − Finally, initiate defuzzification process to form a crisp output.
Advantages of Fuzzy Logic Control
Let us now discuss the advantages of Fuzzy Logic Control.
Cheaper − Developing a FLC is comparatively cheaper than developing model based or other controller in terms of performance.
Robust − FLCs are more robust than PID controllers because of their capability to cover a huge range of operating conditions.
Customizable − FLCs are customizable.
Emulate human deductive thinking − Basically FLC is designed to emulate human deductive thinking, the process people use to infer conclusion from what they know.
Reliability − FLC is more reliable than conventional control system.
Efficiency − Fuzzy logic provides more efficiency when applied in control system.
Disadvantages of Fuzzy Logic Control
We will now discuss what are the disadvantages of Fuzzy Logic Control.
Requires lots of data − FLC needs lots of data to be applied.
Useful in case of moderate historical data − FLC is not useful for programs much smaller or larger than historical data.
Needs high human expertise − This is one drawback as the accuracy of the system depends on the knowledge and expertise of human beings.
Needs regular updating of rules − The rules must be updated with time.
Adaptive Fuzzy Controller
In this chapter, we will discuss what is an Adaptive Fuzzy Controller and how it works. Adaptive Fuzzy Controller is designed with some adjustable parameters along with an embedded mechanism for adjusting them. Adaptive controller has been used for improving the performance of controller.
Basic Steps for Implementing Adaptive Algorithm
Let us now discuss the basic steps for implementing adaptive algorithm.
Collection of observable data − The observable data is collected to calculate the performance of controller.
Adjustment of controller parameters − Now with the help of controller performance, calculation of adjustment of controller parameters would be done.
Improvement in performance of controller − In this step, the controller parameters are adjusted to improve the performance of controller.
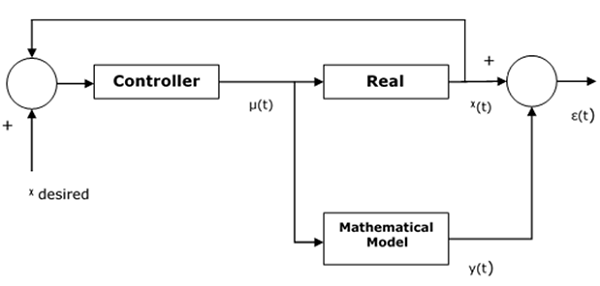
Operational Concepts
Design of a controller is based on an assumed mathematical model that resembles a real system. The error between actual system and its mathematical representation is calculated and if it is relatively insignificant than the model is assumed to work effectively.
A threshold constant that sets a boundary for the effectiveness of a controller, also exists. The control input is fed into both the real system and mathematical model. Here, assume $x\left ( t \right )$ is the output of the real system and $y\left ( t \right )$ is the output of the mathematical model. Then the error $\epsilon \left ( t \right )$ can be calculated as follows −
$$\epsilon \left ( t \right ) = x\left ( t \right ) - y\left ( t \right )$$
Here, $x$ desired is the output we want from the system and $\mu \left ( t \right )$ is the output coming from controller and going to both real as well as mathematical model.
The following diagram shows how the error function is tracked between output of a real system and Mathematical model −
Parameterization of System
A fuzzy controller the design of which is based on the fuzzy mathematical model will have the following form of fuzzy rules −
Rule 1 − IF $x_1\left ( t_n \right )\in X_{11} \: AND...AND\: x_i\left ( t_n \right )\in X_{1i}$
THEN $\mu _1\left ( t_n \right ) = K_{11}x_1\left ( t_n \right ) + K_{12}x_2\left ( t_n \right ) \: +...+ \: K_{1i}x_i\left ( t_n \right )$
Rule 2 − IF $x_1\left ( t_n \right )\in X_{21} \: AND...AND \: x_i\left ( t_n \right )\in X_{2i}$
THEN $\mu _2\left ( t_n \right ) = K_{21}x_1\left ( t_n \right ) + K_{22}x_2\left ( t_n \right ) \: +...+ \: K_{2i}x_i\left ( t_n \right ) $
.
.
.
Rule j − IF $x_1\left ( t_n \right )\in X_{k1} \: AND...AND \: x_i\left ( t_n \right )\in X_{ki}$
THEN $\mu _j\left ( t_n \right ) = K_{j1}x_1\left ( t_n \right ) + K_{j2}x_2\left ( t_n \right ) \: +...+ \: K_{ji}x_i\left ( t_n \right ) $
The above set of parameters characterizes the controller.
Mechanism Adjustment
The controller parameters are adjusted to improve the performance of controller. The process of calculating the adjustment to the parameters is the adjusting mechanism.
Mathematically, let $\theta ^\left ( n \right )$ be a set of parameters to be adjusted at time $t = t_n$. The adjustment can be the recalculation of the parameters,
$$\theta ^\left ( n \right ) = \Theta \left ( D_0,\: D_1, \: ..., \:D_n \right )$$
Here $D_n$ is the data collected at time $t = t_n$.
Now this formulation is reformulated by the update of the parameter set based on its previous value as,
$$\theta ^\left ( n \right ) = \phi ( \theta ^{n-1}, \: D_n)$$
Parameters for selecting an Adaptive Fuzzy Controller
The following parameters need to be considered for selecting an adaptive fuzzy controller −
Can the system be approximated entirely by a fuzzy model?
If a system can be approximated entirely by a fuzzy model, are the parameters of this fuzzy model readily available or must they be determined online?
If a system cannot be approximated entirely by a fuzzy model, can it be approximated piecewise by a set of fuzzy model?
If a system can be approximated by a set of fuzzy models, are these models having the same format with different parameters or are they having different formats?
If a system can be approximated by a set of fuzzy models having the same format, each with a different set of parameters, are these parameter sets readily available or must they be determined online?
Fuzziness in Neural Networks
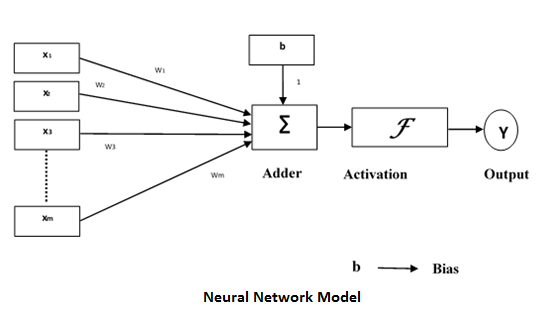
Artificial neural network (ANN) is a network of efficient computing systems the central theme of which is borrowed from the analogy of biological neural networks. ANNs are also named as artificial neural systems, parallel distributed processing systems, connectionist systems. ANN acquires large collection of units that are interconnected in some pattern to allow communications between units. These units, also referred to as nodes or neurons, are simple processors which operate in parallel.
Every neuron is connected with other neuron through a connection link. Each connection link is associated with a weight having the information about the input signal. This is the most useful information for neurons to solve a particular problem because the weight usually inhibits the signal that is being communicated. Each neuron is having its internal state which is called the activation signal. Output signals, which are produced after combining the input signals and the activation rule, may be sent to other units. It also consists of a bias b whose weight is always 1.
Why to use Fuzzy Logic in Neural Network
As we have discussed above that every neuron in ANN is connected with other neuron through a connection link and that link is associated with a weight having the information about the input signal. Hence we can say that weights have the useful information about input to solve the problems.
Following are some reasons to use fuzzy logic in neural networks −
Fuzzy logic is largely used to define the weights, from fuzzy sets, in neural networks.
When crisp values are not possible to apply, then fuzzy values are used.
We have already studied that training and learning help neural networks perform better in unexpected situations. At that time fuzzy values would be more applicable than crisp values.
When we use fuzzy logic in neural networks then the values must not be crisp and the processing can be done in parallel.
Fuzzy Cognitive Map
It is a form of fuzziness in neural networks. Basically FCM is like a dynamic state machine with fuzzy states (not just 1 or 0).
Difficulty in using Fuzzy Logic in Neural Networks
Despite having numerous advantages, there is also some difficulty while using fuzzy logic in neural networks. The difficulty is related with membership rules, the need to build fuzzy system, because it is sometimes complicated to deduce it with the given set of complex data.
Neural-Trained Fuzzy Logic
The reverse relationship between neural network and fuzzy logic, i.e., neural network used to train fuzzy logic is also a good area of study. Following are two major reasons to build neuraltrained fuzzy logic −
New patterns of data can be learned easily with the help of neural networks hence, it can be used to preprocess data in fuzzy systems.
Neural network, because of its capability to learn new relationship with new input data, can be used to refine fuzzy rules to create fuzzy adaptive system.
Examples of Neural-Trained Fuzzy system
Neural-Trained Fuzzy systems are being used in many commercial applications. Let us now see a few examples where Neural-Trained Fuzzy system is applied −
The Laboratory for International Fuzzy Engineering Research (LIFE) in Yokohama, Japan has a back-propagation neural network that derives fuzzy rules. This system has been successfully applied to foreign-exchange trade system with approximately 5000 fuzzy rules.
Ford Motor Company has developed trainable fuzzy systems for automobile idle-speed control.
NeuFuz, software product of National Semiconductor Corporation, supports the generation of fuzzy rules with a neural network for control applications.
AEG Corporation of Germany uses neural-trained fuzzy control system for its water and energy conserving machine. It is having total of 157 fuzzy rules.
Fuzzy Logic - Applications
In this chapter, we will discuss the fields where the concepts of Fuzzy Logic are extensively applied.
Aerospace
In aerospace, fuzzy logic is used in the following areas −
- Altitude control of spacecraft
- Satellite altitude control
- Flow and mixture regulation in aircraft deicing vehicles
Automotive
In automotive, fuzzy logic is used in the following areas −
- Trainable fuzzy systems for idle speed control
- Shift scheduling method for automatic transmission
- Intelligent highway systems
- Traffic control
- Improving efficiency of automatic transmissions
Business
In business, fuzzy logic is used in the following areas −
- Decision-making support systems
- Personnel evaluation in a large company
Defense
In defense, fuzzy logic is used in the following areas −
- Underwater target recognition
- Automatic target recognition of thermal infrared images
- Naval decision support aids
- Control of a hypervelocity interceptor
- Fuzzy set modeling of NATO decision making
Electronics
In electronics, fuzzy logic is used in the following areas −
- Control of automatic exposure in video cameras
- Humidity in a clean room
- Air conditioning systems
- Washing machine timing
- Microwave ovens
- Vacuum cleaners
Finance
In the finance field, fuzzy logic is used in the following areas −
- Banknote transfer control
- Fund management
- Stock market predictions
Industrial Sector
In industrial, fuzzy logic is used in following areas −
- Cement kiln controls heat exchanger control
- Activated sludge wastewater treatment process control
- Water purification plant control
- Quantitative pattern analysis for industrial quality assurance
- Control of constraint satisfaction problems in structural design
- Control of water purification plants
Manufacturing
In the manufacturing industry, fuzzy logic is used in following areas −
- Optimization of cheese production
- Optimization of milk production
Marine
In the marine field, fuzzy logic is used in the following areas −
- Autopilot for ships
- Optimal route selection
- Control of autonomous underwater vehicles
- Ship steering
Medical
In the medical field, fuzzy logic is used in the following areas −
- Medical diagnostic support system
- Control of arterial pressure during anesthesia
- Multivariable control of anesthesia
- Modeling of neuropathological findings in Alzheimer's patients
- Radiology diagnoses
- Fuzzy inference diagnosis of diabetes and prostate cancer
Securities
In securities, fuzzy logic is used in following areas −
- Decision systems for securities trading
- Various security appliances
Transportation
In transportation, fuzzy logic is used in the following areas −
- Automatic underground train operation
- Train schedule control
- Railway acceleration
- Braking and stopping
Pattern Recognition and Classification
In Pattern Recognition and Classification, fuzzy logic is used in the following areas −
- Fuzzy logic based speech recognition
- Fuzzy logic based
- Handwriting recognition
- Fuzzy logic based facial characteristic analysis
- Command analysis
- Fuzzy image search
Psychology
In Psychology, fuzzy logic is used in following areas −
- Fuzzy logic based analysis of human behavior
- Criminal investigation and prevention based on fuzzy logic reasoning