Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Finding the path from one vertex to rest using BFS in C++
In this problem, we are given a directed graph represented as an adjacency list. Our task is to create a program for finding the path from one vertex to rest using BFS.
BFS(Breadth First Search) is an algorithm that traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
Let's take an example to understand the problem,
Input −
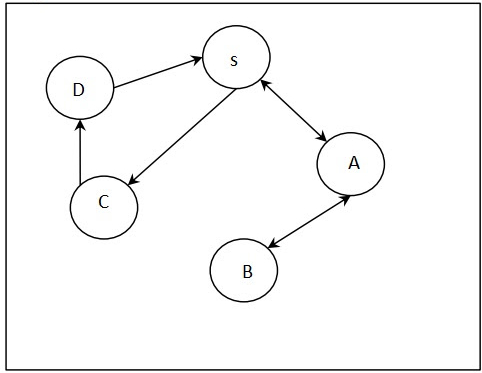
Output
S
A <= S
B <= A <= S
C <= S
D <= C <= S
Solution Approach
To solve the problem, we will be performing the BFS search algorithm on each element of the graph. To perform the task, we will be creating a queue which will be storing the flag for visits to any node. Then, using a visited array we will be checking if the element is visited or not (binary values 0 and 1 denoting the visit).
Now, we will be solving the example step by step to understand the working of our solution,
Starting from node S,
We will directly visit node A.
To reach node B, we will visit node A first then reach node B traversing node A.
To reach node C, we will directly visit C from S.
To reach node D, we will visit node C first and then node D.
Example
Program to illustrate the working of our solution
#include <bits/stdc++.h>
using namespace std;
void printPath(vector<int> parent, int initial, int node){
while (initial != node){
cout<<node<<" <= ";
node = parent[node];
}
cout<<node<<endl;
}
void findPathBFS(vector<vector<int> > graphAdjList, int initial, int graphSize){
vector<int> parent(graphSize, 0);
vector<int> queue(graphSize, 0);
int front = -1, rear = -1;
vector<int> isVisited(graphSize, 0);
isVisited[0] = 1;
parent[0] = initial;
queue[++rear] = initial;
int k;
while (front != rear)
{
k = queue[++front];
for (int j:graphAdjList[k]){
if (isVisited[j] == 0){
queue[++rear] = j;
isVisited[j] = 1;
parent[j] = k;
}
}
}
for (k = 0; k < graphSize; k++)
printPath(parent, initial, k);
}
int main(){
vector<vector<int> > graphAdjList;
graphAdjList.push_back({1, 3});
graphAdjList.push_back({0, 2});
graphAdjList.push_back({1});
graphAdjList.push_back({4});
graphAdjList.push_back({0});
int graphSize = graphAdjList.size();
int initial = 0;
cout<<"The Path from vertex '0' to all other vertex in the graph is : \n";
findPathBFS(graphAdjList, initial, graphSize);
}Output
The Path from vertex '0' to all other vertex in the graph is : 0 1 <= 0 2 <= 1 <= 0 3 <= 0 4 <= 3 <= 0
436 Views
