Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find minimum s-t cut in a flow network in C++
Suppose we have following flow network. As we know an s-t cut is a cut that requires the source s node and a sink t node to be in different subsets, and it includes edges going from the source set to the sink side. Here the capacity of an s-t cut is represented by the sum of each edge capacity in the cut-set. Here we have to find minimum capacity s-t cut of the given network. Here the expected output is all edges of the minimum cut.
So, if the input is like
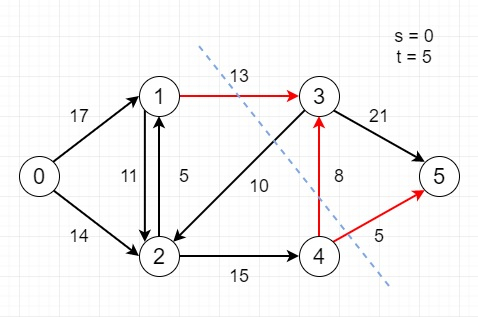
then the output will be [(1,3), (4,3), (4,5)]
To solve this, we will follow these steps −
NODES = 6
Define a function bfs(), this will take graph, src, sink, array par,
Define an array vis of size − NODES. and fill with 0
Define one queue que
insert src into que
vis[src] := true and par[src] := -1
while (que is not empty), do −
u1 := first element of que
delete element from que
for initialize v1 := 0, when v1 < NODES, update (increase v1 by 1), do−
if vis[v1] is false and graph[u1, v1] > 0, then −
insert v1 into que
par[v1] := u1
vis[v1] := true
return true when vis[sink] is true
Define a function dfs(), this will take graph, src, array vis,
vis[src] := true
for initialize i := 0, when i < NODES, update (increase i by 1), do−
if graph[src, i] is non-zero and vis[i] is false, then −
dfs(graph, i, vis)
From the main method, do the following −
Define an array temp_graph and copy graph into it
Define an array par of size: NODES.
while bfs(temp_graph, src, sink, par) is true, do −
path_flow := inf
for initialize v := sink, when v is not equal to src, update v:=par[v], do −
u := par[v]
path_flow := minimum of path_flow and temp_graph[u, v]
for initialize v := sink, when v is not equal to src, update v:=par[v], do −
u := par[v]
temp_graph[u, v] := temp_graph[u, v] - path_flow
temp_graph[v, u] := temp_graph[v, u] + path_flow
Define an array vis of size − NODES. and fill with false
dfs(temp_graph, src, vis)
for initialize i := 0, when i − NODES, update (increase i by 1), do −
for initialize j := 0, when j − NODES, update (increase j by 1), do −
if vis[i] is non-zero and vis[j] is false and graph[i, j] is non-zero, then −
display (i, j) as edge
return
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
#define NODES 6
int bfs(int graph[NODES][NODES], int src, int sink, int par[]) {
bool vis[NODES];
memset(vis, 0, sizeof(vis));
queue <int> que;
que.push(src);
vis[src] = true;
par[src] = -1;
while (!que.empty()) {
int u1 = que.front();
que.pop();
for (int v1=0; v1<NODES; v1++){
if (vis[v1]==false && graph[u1][v1] > 0) {
que.push(v1);
par[v1] = u1;
vis[v1] = true;
}
}
}
return (vis[sink] == true);
}
void dfs(int graph[NODES][NODES], int src, bool vis[]) {
vis[src] = true;
for (int i = 0; i < NODES; i++)
if (graph[src][i] && !vis[i])
dfs(graph, i, vis);
}
void minCut(int graph[NODES][NODES], int src, int sink) {
int u, v;
int temp_graph[NODES][NODES];
for (u = 0; u < NODES; u++)
for (v = 0; v < NODES; v++)
temp_graph[u][v] = graph[u][v];
int par[NODES];
while (bfs(temp_graph, src, sink, par)){
int path_flow = INT_MAX;
for (v=sink; v!=src; v=par[v]) {
u = par[v];
path_flow = min(path_flow, temp_graph[u][v]);
}
for (v=sink; v != src; v=par[v]) {
u = par[v];
temp_graph[u][v] -= path_flow;
temp_graph[v][u] += path_flow;
}
}
bool vis[NODES];
memset(vis, false, sizeof(vis));
dfs(temp_graph, src, vis);
for (int i = 0; i < NODES; i++)
for (int j = 0; j < NODES; j++)
if (vis[i] && !vis[j] && graph[i][j])
cout << "("<< i << ", " << j << ")" << endl;
return;
}
int main() {
int graph1[NODES][NODES] = {
{0, 17, 14, 0, 0, 0},
{0, 0, 11, 13, 0, 0},
{0, 5, 0, 0, 15, 0},
{0, 0, 9, 0, 0, 21},
{0, 0, 0, 8, 0, 5},
{0, 0, 0, 0, 0, 0}
};
minCut(graph1, 0, 5);
}Input
{{0, 17, 14, 0, 0, 0},
{0, 0, 11, 13, 0, 0},
{0, 5, 0, 0, 15, 0},
{0, 0, 9, 0, 0, 21
{0, 0, 0, 8, 0, 5},
{0, 0, 0, 0, 0, 0}};Output
(1, 3) (4, 3) (4, 5)
216 Views
To Continue Learning Please Login