Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find if there is a path of more than k length from a source in C++
Concept
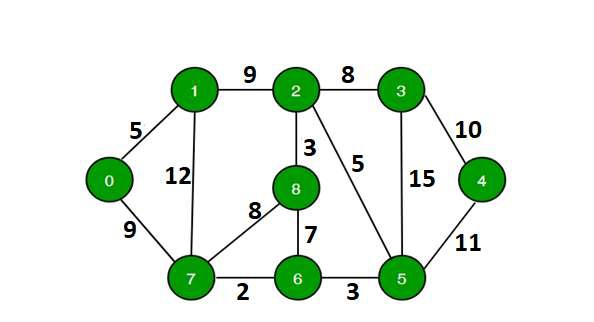
With respect of a given graph, a source vertex in the graph and a number k(here k indicates the path length of graph between source vertex and destination vertex), our task is to determine if there is a simple path (without any cycle) beginning from given source and ending at any other vertex(i.e. destination). The graph is shown in following −
Input
Source s = 0, k = 64
Output
True
There exists a simple path 0 -> 7 -> 1-> 2 -> 8 -> 6 -> 5 -> 3 -> 4, which has a total distance of 68 km which is more than 64.
Input
Source s = 0, k = 70
Output
False
In the above graph, the longest simple path has distance 69 (0 -> 7 -> 1-> 2 -> 3 -> 4 -> 5-> 6 -> 8, so output should be false for any input greater than 69.
Method
It should be noted that one important thing is simply performing BFS(Breadth First Search)or DFS(Depth First Search) and selecting the longest edge at every step would not work.The reason is behind that a shorter edge can produce longer path because of higher weightedges connected through it.
Now the concept is to implement Backtracking. In this case, we begin from given source; traverse all paths from current vertex. Here, we maintain track of current distance from source. It has been seen that if distance becomes more than k, we return true. But in case of alternativeso that if a path doesn’t produces more than k distance, we backtrack.
Now the question is arisen that how do we make sure that the path is simple and we don’tloop in a cycle? Here the concept is to maintain track of current path vertices in an array. In this case, whenever we add a vertex to path, we verify if it already exists or not in current path. It has been seen that if it exists, we ignore the edge.
Example
// Program to find if there is a simple path with
// weight more than k
#include<bits/stdc++.h>
using namespace std;
// iPair ==> Integer Pair
typedef pair<int, int> iPair;
// Now this class represents a dipathted graph using
// adjacency list representation
class Graph{
int V1; // Indicates no. of vertices
// In this case, in a weighted graph, we need to store vertex
// and weight pair for every edge
list< pair<int, int>> *adj1;
bool pathMoreThanKUtil(int src1, int k, vector<bool>&path1);
public:
Graph(int V1); // Shows constructor
// Shows function to add an edge to graph
void addEdge(int u1, int v1, int w1);
bool pathMoreThanK(int src1, int k);
};
// Used to return true if graph has path more than k length
bool Graph::pathMoreThanK(int src1, int k){
// Used to create a path array with nothing included
// in path
vector<bool> path1(V1, false);
// Used to add source vertex to path
path1[src1] = 1;
return pathMoreThanKUtil(src1, k, path1);
}
// Used to print shortest paths from src to all other vertices
bool Graph::pathMoreThanKUtil(int src1, int k, vector<bool>&path1){
// Now if k is 0 or negative, return true;
if (k <= 0)
return true;
//Used to get all adjacent vertices of source vertex src and
// recursively explore all paths from src.
list<iPair>::iterator i;
for (i = adj1[src1].begin(); i != adj1[src1].end(); ++i){
// Used to get adjacent vertex and weight of edge
int v1 = (*i).first;
int w1 = (*i).second;
// Now if vertex v is already there in path, then
// there is a cycle (we ignore this edge)
if (path1[v1] == true)
continue;
// Now if weight of is more than k, return true
if (w1 >= k)
return true;
// Else add this vertex to path
path1[v1] = true;
// Now if this adjacent can provide a path longer
// than k, return true.
if (pathMoreThanKUtil(v1, k-w1, path1))
return true;
// Backtrack
path1[v1] = false;
}
// Now if no adjacent could produce longer path, return
// false
return false;
}
// Used to allocates memory for adjacency list
Graph::Graph(int V1){
this->V1 = V1;
adj1 = new list<iPair> [V1];
}
//Shows utility function to an edge (u, v) of weight w
void Graph::addEdge(int u1, int v1, int w1){
adj1[u1].push_back(make_pair(v1, w1));
adj1[v1].push_back(make_pair(u1, w1));
}
// Driver program to test methods of graph class
int main(){
// Used to create the graph given in above fugure
int V1 = 9;
Graph g(V1);
// making above shown graph
g.addEdge(0, 1, 5);
g.addEdge(0, 7, 9);
g.addEdge(1, 2, 9);
g.addEdge(1, 7, 12);
g.addEdge(2, 3, 8);
g.addEdge(2, 8, 3);
g.addEdge(2, 5, 10);
g.addEdge(3, 4, 10);
g.addEdge(3, 5, 15);
g.addEdge(4, 5, 11);
g.addEdge(5, 6, 3);
g.addEdge(6, 7, 2);
g.addEdge(6, 8, 7);
g.addEdge(7, 8, 8);
int src1 = 0;
int k = 70;
g.pathMoreThanK(src1, k)? cout << "Yes\n" :
cout << "No\n";
k = 68;
g.pathMoreThanK(src1, k)? cout << "Yes\n" :
cout << "No\n";
return 0;
}Output
No Yes
89 Views
