Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain the conversions of expressions of stacks in C language
Stack is a linear data structure, where data is inserted and removed only at one end.
Algorithms
Given below is an algorithm for Push ( ) −
- Check for stack overflow.
if (top = = n-1)
printf("stack over flow");- Otherwise, insert an element into the stack.
top ++ a[top] = item
Given below is an algorithm for Pop ( ) −
- Check for stack underflow.
if (top = = -1)
printf("stack under flow");Otherwise, delete an element from the stack.
item = a[top] top --
Given below is an algorithm for Display ( ) −
if (top == -1)
printf ("stack is empty");Otherwise, follow the below mentioned algorithm.
for (i=0; i<top; i++)
printf ("%d", a[i]);Application of stacks
Let us understand the conversions of expressions of stacks in C language.
Expression − It is a legal combination of operands and operations.
Types of expressions
There are three types of expressions in C language on which the conversions and evaluations can be carried out. They are explained below −
Infix expression − Operator is in between the operands. For example, A+B
Prefix expression − Operator is before the operands. For example, +AB
Postfix expression − Operator is after the operands. For example, AB+
Conversion of infix to postfix and infix to prefix is explained below −
Infix to postfix Infix to prefix A+ B*C A+ B*C A+ BC * A+ *BC ABC* + +A*BC
For example,
Convert A+B*C / D-E+F infix to postfix and prefix.
Infix to prefix Infix to postfix A +B*C / D-E+F A +B*C / D-E+F A +*BC / D-E+F A +BC* / D-E+F A + / *BCD -E+F A +BC*D /-E+F +A /*BCD -E +F ABC *D /+ -E+F -+A/*BCDE +F ABC *D/ +E- +F + - +A/*BCDEF ABC *D / +E –F+
Algorithm
Scan the input string from left to right and follow the steps given below −
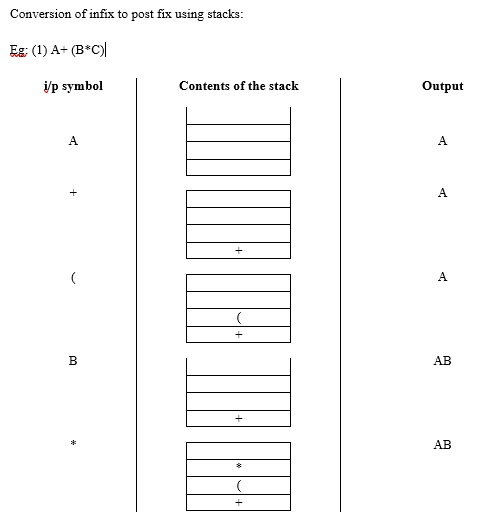
Step 1 − If the input symbol is an operand, print it on to the monitor.
Step 2 − If the input symbol is ‘(‘then, push it on to the stack.
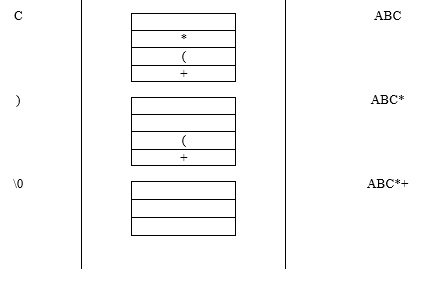
Step 3 − If the input the symbol is ‘)’ then, pop out all the contents of the stack until you get ‘(‘.
Step 4 − If the input symbol is an operator, check with the priority of the operator on top of the stack with the current input symbol.
If the top priority of top of the stack is greater than or equal to the priority of the current symbol, then pop out the content of the stack and put the current symbol in to the stack.
Otherwise, push the operator on to the stack.
Step 5 − If the input symbol is ‘\0’ then, pop out the contents of the stack until it becomes empty.
Conversion of infix to post fix with the help of stacks is given below −
1K+ Views
