Explain deleting an element in a queue by using C language

Data structure is collection of data organized in a structured way. It is divided into two types as explained below −

• Linear data structure − Data is organized in a linear fashion. For example, arrays, structures, stacks, queues, linked lists.

• Nonlinear data structure − Data is organized in a hierarchical way. For example, Trees, graphs, sets, tables.

Also Read: Data Structures and Types

Queue

Queue is a linear data structure, where the insertion is done at rear end and the deletion is done at the front end.

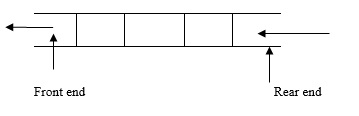
The order of queue is FIFO – First In First Out

Operations

• Insert – Inserting an element into a queue.
• Delete – Deleting an element from the queue.

Conditions

• Queue over flow − Trying to insert an element into a full queue.

• Queue under flow − Trying to delete an element from an empty queue.

Algorithms

Given below is an algorithm for insertion ( ) −

• Check for queue overflow.

if (r==n)
printf ("Queue overflow")

• Otherwise, insert an element in to the queue.

q[r] = item
r++

Given below is an algorithm for deletion ( ) −

• Check for queue under flow.

if (f==r)
printf ("Queue under flow")

• Otherwise, delete an element from the queue.

item = q[f]
f++

Given below is an algorithm for display ( ) −

• Check whether the queue is empty or not.

if (f==r)
printf("Queue is empty")

• Otherwise, print all the elements from ‘f’ to ‘r’.

for(i=f; i<r; i++)
printf ("%d", q[i]);

C program for deleting an element in queue

Following is the C program for deleting an element in queue −

#include <stdio.h>
#define MAX 50
void insert();
int array[MAX];
int rear = - 1;
int front = - 1;
main(){
   int add_item;
   int choice;
   while (1){
      printf("1.Insert element to queue 
");
      printf("2.Delete an element from queue
");
      printf("3.Display elements of queue 
");
      printf("4.Quit 
");
      printf("Enter your choice : ");
      scanf("%d", &choice);
      switch (choice){
         case 1:
            insert();
         break;
         case 2:
            delete();
         case 3:
            display();
         break;
         case 4:
            exit(1);
         default:
         printf("Wrong choice 
");
      }
   }
}
void insert(){
   int add_item;
   if (rear == MAX - 1)
      printf("Queue Overflow 
");
   else{
      if (front == - 1)
      /*If queue is initially empty */
      front = 0;
      printf("Inset the element in queue : ");
      scanf("%d", &add_item);
      rear = rear + 1;
      array[rear] = add_item;
   }
}
void display(){
   int i;
   if (front == - 1)
      printf("Queue is empty 
");
   else{
      printf("Queue is : 
");
      for (i = front; i <= rear; i++)
         printf("%d ", array[i]);
         printf("
");
   }
}
void delete(){
   if (front == - 1 || front > rear){
      printf("Queue Underflow 
");
      return ;
   }
   else{
      printf("Element deleted from queue is : %d
",array[front]);
      front = front + 1;
   }
}

Output

When the above program is executed, it produces the following result −

1.Insert element to queue
2.Delete an element from queue
3.Display elements of queue
4.Quit
Enter your choice: 1
Inset the element in queue: 12
1.Insert element to queue
2.Delete an element from queue
3.Display elements of queue
4.Quit
Enter your choice: 1
Inset the element in queue: 23
1.Insert element to queue
2.Delete an element from queue
3.Display elements of queue
4.Quit
Enter your choice: 1
Inset the element in queue: 34
1.Insert element to queue
2.Delete an element from queue
3.Display elements of queue
4.Quit
Enter your choice: 2
Element deleted from queue is: 12
Queue is:
23 34
1.Insert element to queue
2.Delete an element from queue
3.Display elements of queue
4.Quit
Enter your choice: 2
Element deleted from queue is: 23
Queue is:
34
1.Insert element to queue
2.Delete an element from queue
3.Display elements of queue
4.Quit
Enter your choice: 4