Estimation of gaussian noise in noisy image using MATLAB

In digital images, the gaussian noise is a type of noise that follows a normal or Gaussian distribution. In a digital image, the gaussian noise is visualized as a random variation in pixel intensities. The estimation of gaussian noise is one of the important tasks in digital image processing utilized to perform various operations such as denoising, image restoration, and more.

Methods of Estimating Gaussian Noise in Digital Image

We can estimate the Gaussian noise in a digital image using various methods. The following are some commonly used methods for estimating the gaussian noise.

• Standard Deviation Method

• Histogram Analysis

Let us discuss these two methods in detail with the help of examples.

Estimating Gaussian Noise Using Standard Deviation Method

In digital image processing, the standard deviation method is the simplest method of estimating the gaussian noise. It estimates the gaussian noise in the image by finding the standard deviation of pixel intensity values.

The step-by-step process of estimating the gaussian noise in a digital image using the standard deviation method is explained below.

• Step (1) − Read the input image having gaussian noise.

• Step (2) − Convert the image to grayscale if required.

• Step (3) − Convert the image to double data type for calculations.

• Step (4) − Estimate the gaussian noise by computing the standard deviation of image pixel intensities.

• Step (5) − Display the estimated gaussian noise.

• Step (6) − Display the noisy and denoised images for visual analysis.

In MATLAB, the estimation of gaussian noise through the standard deviation method is a six-step straightforward method.

Example

Let us take an example to understand the code implementation to estimate the gaussian noise using MATLAB.

% MATLAB code to estimate gaussian noise using standard deviation method
% Read the noisy image
noisy_img = imread('Noisy_Image.jpg');

%Convert the input noisy image to grayscale
gray_img = rgb2gray(noisy_img);

% Convert the gray image to double data type
gray_img = im2double(gray_img);

% Estimate the Gaussian noise using standard deviation
estimated_noise = std2(gray_img);

% Display the estimated gaussian noise in the image
disp(['Estimated Gaussian Noise in the Image is: ' num2str(estimated_noise)]);

% Remove the noise from the image
denoised_img = imgaussfilt(gray_img, 2);

% Display the noisy and denoised images
figure;
subplot(1, 2, 1);
imshow(gray_img);
title('Noisy Image');

subplot(1, 2, 2);
imshow(denoised_img);
title('Denoised Image');

Output

Estimated Gaussian Noise in the Image is: 0.25054

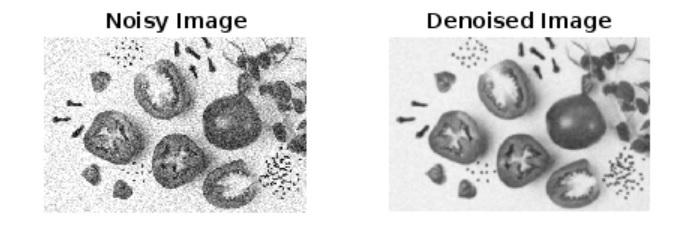
Explanation

In this MATLAB example, we have estimated the gaussian noise in the image using the standard deviation method.

• In the code, we start by reading the noisy image using the "imread" function. Then, we convert the input image to grayscale and double datatype for calculations using the "rgb2gray" and "im2double" functions respectively.

• After that we estimate the gaussian noise in the image using the "std2" function. This function calculates the standard deviation of the pixel intensity values of the noisy image.

• Next, we display the estimated gaussian noise in the image using the "disp" function.

• In the next step, we also remove the gaussian noise using the gaussian filter and display the noisy and denoised images for visual comparison.

This is how we can estimate the gaussian noise using the standard deviation method in MATLAB.

Estimating Gaussian Noise Using Histogram Analysis

In MATLAB, we can estimate the gaussian noise in a digital image by analyzing the histogram of the image. In this method, we analyze the distribution of pixel intensity values in image. Then, we can use these estimated values to denoise the image.

The steps involved in estimating the gaussian noise in an image using the histogram analysis are explained below.

• Step (1) − Read the noisy image using the "imread" function.

• Step (2) − Convert the input image to grayscale for histogram analysis.

• Step (3) − Compute and display the histogram of the image.

• Step (4) − Fit the gaussian distribution of the noisy image.

• Step (5) − Determine the mean value and standard deviation of the fitted gaussian distribution of the noisy image.

• Step (6) − Display the estimated gaussian noisy i.e., mean value and standard deviation of the noisy image.

• Step (7) − Denoise the image.

• Step (8) − Display the noisy and denoised images for visual comparison.

Example

Let us take an example to understand the implementation of these steps to estimate the gaussian noise in an image.

% MATLAB code to estimate gaussian noise using histogram analysis
% Read the noisy image
noisy_img = imread('noisy_image.jpg');

% Convert to the noisy image to grayscale
gray_img = rgb2gray(noisy_img);

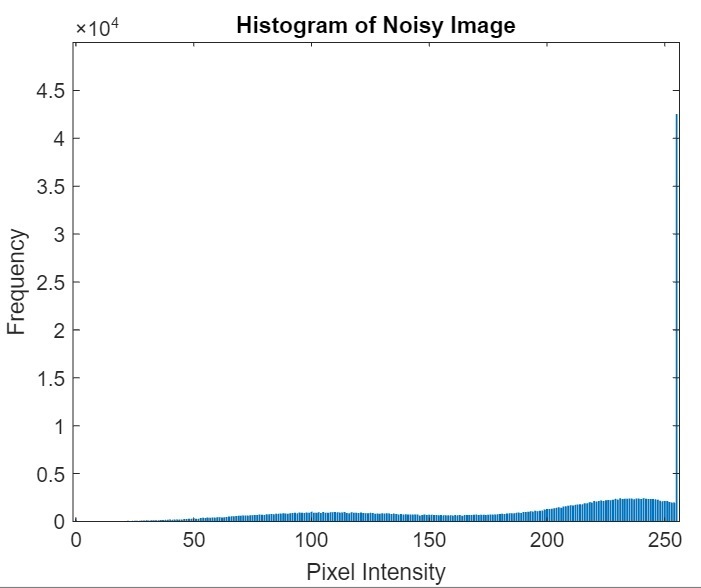
% Compute the histogram of the noisy image
[counts, binLocations] = imhist(gray_img);

% Display the histogram of noisy image
figure;
bar(binLocations, counts);
title('Histogram of Noisy Image');
xlabel('Pixel Intensity');
ylabel('Frequency');

% Fit gaussian distribution to pixel intensity values
g = fitdist(gray_img(:), 'Normal');

% Estimate the mean value and standard deviation
mean_value = g.mu;
std_dev = g.sigma;

% Display estimated gaussian noise parameters
fprintf('Estimated Mean Value: %.2f
', mean_value);
fprintf('Estimated Standard Deviation: %.2f
', std_dev);

% Denoise the image using the gaussian filter
denoised_img = imgaussfilt(gray_img, 1.5);

% Display the noisy and denoised images
figure;
subplot(1, 2, 1);
imshow(noisy_img);
title('Noisy Image');

subplot(1, 2, 2);
imshow(denoised_img, []);
title('Denoised Image');

Output

When you run this code, it will produce the following output −

Histogram −

Noise Parameters −

Estimated Mean Value: 187.94
Estimated Standard Deviation: 12.03

Noisy and Denoised Images −

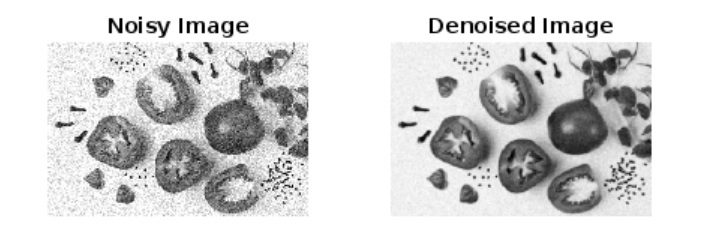
This example demonstrates the step-by-step process of estimating gaussian noise in an image using the histogram analysis method.

Conclusion

This is all about estimation of gaussian noise in noisy image using MATLAB. Estimation of gaussian noise is a crucial task in digital image processing. It is helpful in denoising a noisy image. MATLAB provides several methods to estimate the gaussian noise in a noisy image. But the most commonly used methods are standard deviation method and histogram analysis method. In this tutorial, I explained both the methods in detail with the help of examples in MATLAB programming.