Energy Stored in a Capacitor – Formula and Examples

A capacitor is an electronic circuit component that stores electrical energy in the form of electrostatic charge. Thus, a capacitor stores the potential energy in it. This stored electrical energy can be obtained when required. Ideally, a capacitor does not dissipate energy, but stores it.

A typical capacitor consists of two metallic plates separated by an insulating material, called dielectric. When these two metallic plates of the capacitor are connected to a source of electrical energy, the capacitor starts charging and stores electrical energy in its dielectric. Therefore, it is important to derive the expression of this stored energy in the capacitor so that we can select a suitable capacitor for our circuit designing.

Energy Stored in a Capacitor

As discussed above, a capacitor stores electrical energy in the form of electrostatic charge. Thus, a charged capacitor produces an electrostatic field. When the capacitor of capacitance C farad is connected across a battery of V volts as shown in Figure-1. In this situation, the entire battery voltage V is applied across the capacitor plates. As a result, plate A of the capacitor becomes positively charged while plate B becomes negatively charged. This potential difference between the two plates establishes an electric field directed from plate A to B through the dielectric material of the capacitor.

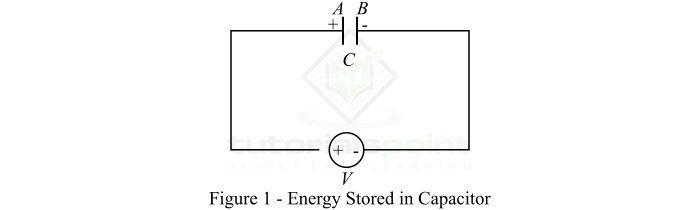
Due to this electric force, the end of the dielectric near the positive plate will become negatively polarized, while the end near the negative plate will become positively polarized. Consequently, there is an electrostatic charge (and electrostatic field) is created within the capacitor. In this condition, the capacitor is said to be charged and stores a finite amount of energy.

Now, let us derive the expression of energy stored in the capacitor. For that, let at any stage of charging, the electric charge stored in the capacitor is q coulombs and the voltage the plates of the capacitor is v volts. Then,

$$\mathrm{q\propto v}$$

$$\mathrm{\Rightarrow q=C v}$$

By the definition of voltage, a work of v Joules is required to be done in storing a charge of 1 Coulomb in the capacitor. Hence, for storing a charge of dq Coulombs in the capacitor, the work done is,

$$\mathrm{dW=v\, dq}$$

$$\mathrm{\Rightarrow dW=v\, d\left ( Cv \right )}$$

$$\mathrm{\therefore dW=Cv\, dv}$$

Integrating on both side to get the total work done in raising the voltage of the uncharged capacitor to V volts.

$$\mathrm{W=C\int_{0}^{v}v\, dv=C\left [ \frac{v^{2}}{2} \right ]_{0}^{v}}$$

$$\mathrm{\therefore W=\frac{1}{2}CV^{2}}$$

This work done will be stored in the capacitor in the form of potential energy (electrostatic field).

Also,

$$\mathrm{C=\frac{Q}{V}\: and\: V=\frac{Q}{C}}$$

Thus, the energy stored in the capacitor can also be given by,

$$\mathrm{W=\frac{1}{2}QV=\frac{1}{2}\frac{Q^{2}}{C}}$$

The energy stored in the capacitor will be expressed in joules if the charge Q is given in coulombs, C in farad, and V in volts.

From equations of the energy stored in a capacitor, it is clear that the energy stored in a capacitor does not depend on the current through the capacitor.

Note − A pure or ideal capacitor does not dissipate energy, instead, it stores energy and returns the stored energy when delivering power to the circuit.

Numerical Example (1)

A capacitor has a capacitance of 0.5 μF is connected across a battery of 120 V. Determine the energy stored in the capacitor.

Solution

Given data,

• 𝐶 = 0.5 μF = 0.5 × 10⁻⁶F
• 𝑉 = 120 V

The energy stored in the capacitor will be,

$$\mathrm{W=\frac{1}{2}CV^{2}=\frac{1}{2}\times \left ( 0.5\times 10^{-6} \right )\times 120}$$

$$\mathrm{\therefore W=3\times 10^{-5}J=30\, \mu J}$$

Numerical Example (2)

When a capacitor is connected to a source of 240 V, it stores a charge of 50 mC. Calculate the energy stored in the capacitor.

Solution

Given data,

• Voltage, 𝑉 = 240 V
• Charge, 𝑄 = 50 mC = 50 × 10⁻³ C

The energy stored in the capacitor is given by,

$$\mathrm{W=\frac{1}{2}QV=\frac{1}{2}\times \left ( 50\times 10^{-3} \right )\times 240}$$

$$\mathrm{\therefore W=6\, Joules}$$

Conclusion

From the above discussion, it is clear that a capacitor stores electrical energy in the form of electrostatic field, and this stored energy is referred to as potential energy because it is due to the difference of potential.

From the expression of stored energy in a capacitor, it is clear that the energy stored is directly proportional to capacitance of the capacitor, which means a capacitor of higher capacitance can store more amount of energy for the same voltage and vice-versa.

Due to their energy-storing property, capacitors are used in several electrical and electronic circuits such as chargers, capacitor banks, computer circuits, etc.