Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Economic Choice of Conductor Size – Kelvin’s Law (Economics of Power Transmission)
The cost of conductor material required for designing a transmission line is a very considerable part of the total cost of a transmission line. Therefore, the determination of proper size of the conductor for the transmission line is very important. The proper size of the conductor for transmission line is determined by the Kelvin’s law (given by Lord Kelvin in 1881).
The Kelvin’s law states that the most economical area of conductor is that for which the total annual cost of transmission line is minimum.
The total annual cost of the transmission line can be divided into two parts viz. −
- Annual charges on capital cost
- Annual cost of energy wasted in conductor
Annual Charges on Capital Cost
These annual charges are on the account of interest and depreciation on the capital cost of complete installation of the transmission line. In case of overhead transmission system, the complete installation cost will be the annual interest and depreciation on the capital cost of conductors, pole supports and insulators and also the cost of their erection.
Now, for the overhead transmission system, the cost of conductor is proportional to the area of cross-section, the cost of insulator is constant and the cost of pole (or tower) supports and their erection is partly constant and partly proportional to cross-sectional area of the conductor.
Therefore, the annual charges on the capital cost of an overhead transmission line can be expressed as −
$$\mathrm{Annual\: Charges\mathit{\mathrm{\, =\, } P_{\mathrm{1}}\mathrm{\, +\, }aP_{\mathrm{2}}\; \; \; \cdot \cdot \cdot \left ( \mathrm{1} \right )}}$$
Where, P1 and P2 are the constants and a is the cross-sectional area of the conductor.
Annual Cost of Energy Wasted in Conductor
This cost is on the account of energy wasted in the conductor due to I2R losses. Suppose a constant current in the conductor throughout the year, thus the power loss in the conductor is directly proportional to the resistance. Since, the resistance of the conductor is inversely proportional to the cross-sectional area of the conductor. Hence, the energy lost in the conductor is inversely proportional to the cross-sectional area.
Therefore, the annual cost of energy wasted in the conductor of overhead transmission line can be expressed as −
$$\mathrm{Annual\: cost \: of \: energy \: lost\mathit{\mathrm{\, =\, }\frac{P_{\mathrm{3}}}{a}\; \; \;\cdot \cdot \cdot \left ( \mathrm{2} \right ) }}$$
Where, P3 is a constant.
Now, from the equations (1) and (2), the total annual cost of the transmission line is given by,
$$\mathrm{Total \: annual \: cost\: of \: line,\: \mathit{Y\mathrm{\, =\, }P_{\mathrm{1}}\mathrm{\, +\, }aP_{\mathrm{2}}\mathrm{\, +\, }\frac{P_{\mathrm{3}}}{a}\; \; \; \cdot \cdot \cdot \left ( \mathrm{3} \right ) }}$$
Therefore, the total annual cost of transmission line will be minimum, when the differentiation of Y with respect to the variable (i.e. a) is zero, i.e.
$$\mathrm{\mathit{\frac{dY}{da}}\mathrm{\, =\, }0}$$
$$\mathrm{\mathit{\Rightarrow \frac{d}{da}\left ( P_{\mathrm{1}}\mathrm{\, +\, }aP_{\mathrm{2}}\mathrm{\, +\, }\frac{P_{\mathrm{3}}}{a} \right )}\mathrm{\, =\, }0}$$
$$\mathrm{\mathit{\Rightarrow \mathrm{0}\mathrm{\, +\, }P_{\mathrm{2}}-\frac{P_{\mathrm{3}}}{a^{\mathrm{2}}}}\mathrm{\, =\, }0}$$
$$\mathrm{\mathit{\Rightarrow aP_{\mathrm{2}}\mathrm{\, =\, }\frac{P_{\mathrm{3}}}{a}}\; \; \; \cdot \cdot \cdot \left ( 4 \right )}$$
i.e.,
$$\mathrm{Variable\: part\: of \: annual\: charges\: on \: capital\: cost\, =\, Annual \: cost \: of\: energy\: wasted}$$
Hence, the Kelvin’s law can also be stated as the most economical area of conductor is that for which the variable part of annual charges on capital cost is equal to the annual cost of energy wasted in the conductor.
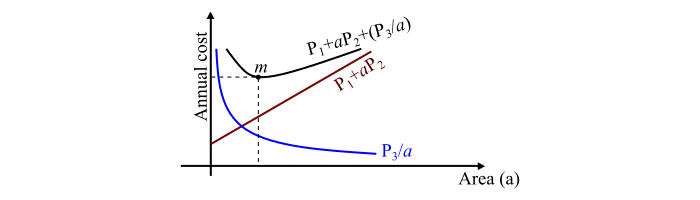
The figure shows the graphical representation of the Kelvin’s law. Here, m is the lowest point on the curve, which represents the most economical area of cross-section, i.e., lowest annual cost of transmission line.
Limitations of Kelvin’s Law
In practice, the following are the limitations of the Kelvin’s law −
The Kelvin’s law does not involve several physical factors such as safe current density, mechanical strength, corona loss, etc.
The conductor size determined by the Kelvin’s law may not always be practicable one since it may be too small for the safe carrying of necessary current.
It is not easy to estimate the energy loss in the transmission line without actual load curves, which are not available at the time of estimation.
The assumption that the annual charges on the account of interest and depreciation on the capital cost is in the form of 𝑃1 + 𝑎𝑃2 is strictly speaking not true. Therefore, the interest and depreciation on the capital cost cannot be determined accurately.
7K+ Views
