Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Diminishing Value Method of Calculating Depreciation
Depreciation of Power Plant Equipment
The reduction in the value of the equipment and other property of the power station every year is known as depreciation. Therefore, a suitable amount, called depreciation charge, must be set aside annually so that by the time the life span of the power plant is over, the collected amount equals to the cost of the replacement of the power plant.
Diminishing Value Method of Depreciation
In the diminishing value method for calculating the depreciation, the depreciation charge is made every year at a fixed rate on the diminished value of the equipment, i.e. the depreciation charge is first applied to the initial cost of equipment and then to its diminished value.
For example, consider the initial cost of an equipment is Rs. 100000 and its scrap value after the useful life is 0. If the rate of depreciation per annum is 10%. Then, the depreciation charge for the first year will be
$$\mathrm{First\: year \: depreciation \: charge = 100000 \times 10\% \, =\, Rs. 10000}$$
Thus, the value of the equipment is diminished by Rs 10000 and becomes Rs 90000.
For the second year, the depreciation charge will be made on the diminished value, i.e., Rs 90000 and it will be,
$$\mathrm{=90000\times 10\%\, =\, Rs.9000}$$
Now, the value of the equipment becomes 90000 − 9000 = Rs. 81000
Similarly, for the third year, the depreciation charge will be,
$$\mathrm{= 81000 \times 10\% \, =\, Rs. 8100}$$
Mathematical Explanation
Let
- 𝑃 = Initial cost of the equipment
- 𝑆 = Scrap value of the equipment after useful life
- 𝑛 = Useful life of the equipment in years
- 𝑥 = Annual unit depreciation
Then, the value of the equipment after one year is,
$$\mathrm{Value\: after\: 1\: year \: =\: \mathit{P-Px\mathrm{\, =\, }P\left ( \mathrm{1} -x\right )}}$$
And, value of equipment after two years is,
$$\mathrm{Value\: after\: 2\: years \, =\, Diminished\: value - Annual\: depreciation}$$
$$\mathrm{\Rightarrow Value\: after\: 2 \: years \, =\, \mathit{\left ( P-Px \right )-\left [\left ( P-Px \right )x \right ]}}$$
$$\mathrm{\Rightarrow Value\: after\: 2 \: years \, =\,\mathit{\left ( P-Px \right )\left ( \mathrm{1}-x \right )\mathrm{\, =\, }P\left ( \mathrm{1}-x\right )\left ( \mathrm{1}-x\right )}}$$
$$\mathrm{\therefore Value\: after\: 2 \: years \, =\, \mathit{P\left ( \mathrm{1}-x\right )^{\mathrm{2}}}}$$
Hence, the value of equipment after 𝑛 years is,
$$\mathrm{Value\: after\: \mathit{n} \: years \, =\, \mathit{P\left ( \mathrm{1}-x\right )^{n}}}$$
Also, the value of equipment after useful life (i.e., n years) is equal to the scrap value (S).
$$\mathrm{\mathit{\therefore S\mathrm{\, =\, }P\left ( \mathrm{1}-x \right )^{n}}}$$
$$\mathrm{\mathit{\Rightarrow \left ( \mathrm{1}-x \right )^{n}\mathrm{\, =\, }\frac{S}{P}}}$$
$$\mathrm{\mathit{\Rightarrow \left ( \mathrm{1}-x \right )\mathrm{\, =\, }\left ( \frac{S}{P} \right )^{\mathrm{1}/n}}}$$
$$\mathrm{\mathit{\therefore x\mathrm{\, =\, }\mathrm{1}-\left ( \frac{S}{P} \right )^{\mathrm{1}/n}}}$$
The above expression gives the value of the annual depreciation.
Therefore, the depreciation charge to be made for the first year is given by,
$$\mathrm{Depriciation\: charge\: for\: 1^{st} \: year\mathit{\mathrm{\, =\, }Px\mathrm{\, =\, }P\left [ \mathrm{1}-\left ( \frac{S}{P} \right )^{\mathrm{1}/n} \right ]}}$$
Similarly, the annual depreciation charge for any number of years can be calculated.
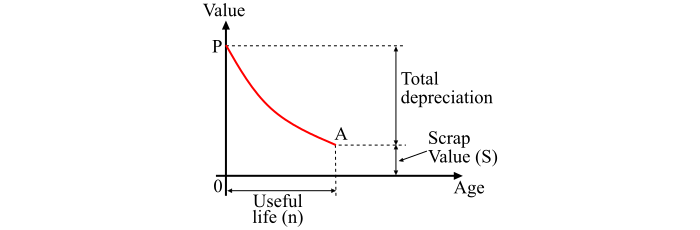
The graphical representation of diminishing value method for calculating depreciation is shown in the figure. From the figure, it is clear that the initial value of equipment reduces, through depreciation, to the scrap value over the useful life of the equipment. Therefore, the depreciation curve follows the path PA. Also, it can be observed that the depreciation charges are heavy in the early years but decreases to a low value in the later years.
The diminishing value method suffers from drawbacks as −
Low depreciation charges are made in the late years when the maintenance charges are very high.
The depreciation charge is independent of the rate of interest which it may draw during accumulation. Such interest moneys are to be considered as income.
Numerical Example
A transformer costing Rs 150000 and has a scrap value of Rs 15000 at the end of 25 years. Determine the depreciated value of the transformer at the end of 20 years by using diminishing value method.
Solution
Given,
- Initial cost of transformer, 𝑃 = Rs. 150000
- Scrap value of transformer, 𝑆 = Rs. 15000
- Useful life, 𝑛 = 25 years
Then, Annual unit depreciation,
$$\mathrm{\mathit{x\mathrm{\, =\, }x\mathrm{\, =\, }\mathrm{1}-\left ( \frac{S}{P} \right )^{\mathrm{1}/n}\mathrm{\, =\, }\mathrm{1-\left ( \frac{15000}{150000} \right )^{1/25}}}}$$
$$\mathrm{\mathit{\therefore x}\mathrm{\, =\, }1-0.912\mathrm{\, =\, }0.088}$$
Therefore,
$$\mathrm{Value\: of\: transformer\: after\: 20\: years \mathit{\mathrm{\, =\, }P\left ( \mathrm{1}-x \right )^{\mathrm{20}}}} $$
$$\mathrm{\mathrm{\, =\, } 150000 \times \left ( 1 - 0.088 \right )^{20} \mathrm{\, =\, } Rs. 23767.74}$$
3K+ Views
