Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Design a DFA of a string with at least two 0’s and at least two 1’s
A Deterministic Finite automaton (DFA) is a 5-tuples
M=(Q, Σ, δ,q0,F)
Where,
- Q : Finite set called states.
- Σ : Finite set called alphabets.
- δ : Q × Σ → Q is the transition function.
- q0 ϵ Q is the start or initial state.
- F : Final or accept state.
Problem
Construct DFA of a string with at least two 0’s and at least two 1’s.
Solution
The language generated based on the given condition over the alphabet Σ ={0,1) is −
L={0011,001011,0001010,0011001,010101,……}
The given language accepts at least two zero’s means it can accept two or more than two zero’s and at least two one’s means it accepts two or more than two one’s.
Suppose,
- Input − 00010
- Output − string rejected
Because, the given input does not have at least two’s.
Even though it has at least zeros, it won’t accept the string.
To accept the string both conditions are satisfied, if one fails the string will not be accepted by the machine.
- Input − 001001001
- Output − string accepted
Now construct the DFA for given inputs −
| State | Number of zero’s | Number of one's |
|---|---|---|
| → q0 | 0 | 0 |
| q1 | 0 | 1 |
| q2 | 0 | > =2 |
| q3 | 1 | 0 |
| q4 | 1 | 1 |
| q5 | 1 | > =2 |
| q6 | > =2 | 0 |
| q7 | > =2 | 1 |
| *q8 | > =2 | > =2 |
The DFA will be as follows −
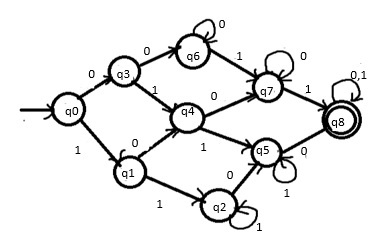
Explanation
If input is 1 then the number of 1 increases to 1. Move to state q1. If input is 0 then the number of 0 increases to 1. Move to state q3.
If input is 1 then the number of 1 increases to 2. Move to state q2. If input is 0 then the number of 0 increases to 1. Move to state q4.
If input is 1 then the number of 1 always increases by 1. And then remain in the same state. If input is 0 then the number of 0 increases to 1. Move to state q5.
If input is 1 then the number of 1 increases to 1. Move to state q4. If input is 0 then the number of 0 increases to 2. Move to state q6.
If input is 1 then the number of 1 increases to 2. Move to state q5. If input is 0 then number of 0 increases to 2. Move to state q7.
If input is 1 then the number of 1 always increases by 1. And then remain in the same state. If input is 0 then the number of 0 increases to 2. Move to state q8
If input is 1 then the number of 1 increase to 1. Move to state q7. If input is 0 then the number of 0 keeps increasing by 1. And then remain in the same state.
If input is 1 then the number of 1 increase to 2. Move to state q8. If input is 0 then the number of 0 keeps increasing by 1. And then remain in the same state.
If input is 1 then the number of 1 always increases by 1. And then remain in the same state. If input is 0 then the number of 0 keeps increasing by 1. And then remain in the same state.
Finally, if the string is finished, then it is ACCEPTED.
2K+ Views
