
- Data Mining - Home
- Data Mining - Overview
- Data Mining - Tasks
- Data Mining - Issues
- Data Mining - Evaluation
- Data Mining - Terminologies
- Data Mining - Knowledge Discovery
- Data Mining - Systems
- Data Mining - Query Language
- Classification & Prediction
- Data Mining - Decision Tree Induction
- Data Mining - Bayesian Classification
- Rules Based Classification
- Data Mining - Classification Methods
- Data Mining - Cluster Analysis
- Data Mining - Mining Text Data
- Data Mining - Mining WWW
- Data Mining - Applications & Trends
- Data Mining - Themes
Data Mining - Quick Guide
Data Mining - Overview
There is a huge amount of data available in the Information Industry. This data is of no use until it is converted into useful information. It is necessary to analyze this huge amount of data and extract useful information from it.
Extraction of information is not the only process we need to perform; data mining also involves other processes such as Data Cleaning, Data Integration, Data Transformation, Data Mining, Pattern Evaluation and Data Presentation. Once all these processes are over, we would be able to use this information in many applications such as Fraud Detection, Market Analysis, Production Control, Science Exploration, etc.
What is Data Mining?
Data Mining is defined as extracting information from huge sets of data. In other words, we can say that data mining is the procedure of mining knowledge from data. The information or knowledge extracted so can be used for any of the following applications −
- Market Analysis
- Fraud Detection
- Customer Retention
- Production Control
- Science Exploration
Data Mining Applications
Data mining is highly useful in the following domains −
- Market Analysis and Management
- Corporate Analysis & Risk Management
- Fraud Detection
Apart from these, data mining can also be used in the areas of production control, customer retention, science exploration, sports, astrology, and Internet Web Surf-Aid
Market Analysis and Management
Listed below are the various fields of market where data mining is used −
Customer Profiling − Data mining helps determine what kind of people buy what kind of products.
Identifying Customer Requirements − Data mining helps in identifying the best products for different customers. It uses prediction to find the factors that may attract new customers.
Cross Market Analysis − Data mining performs Association/correlations between product sales.
Target Marketing − Data mining helps to find clusters of model customers who share the same characteristics such as interests, spending habits, income, etc.
Determining Customer purchasing pattern − Data mining helps in determining customer purchasing pattern.
Providing Summary Information − Data mining provides us various multidimensional summary reports.
Corporate Analysis and Risk Management
Data mining is used in the following fields of the Corporate Sector −
Finance Planning and Asset Evaluation − It involves cash flow analysis and prediction, contingent claim analysis to evaluate assets.
Resource Planning − It involves summarizing and comparing the resources and spending.
Competition − It involves monitoring competitors and market directions.
Fraud Detection
Data mining is also used in the fields of credit card services and telecommunication to detect frauds. In fraud telephone calls, it helps to find the destination of the call, duration of the call, time of the day or week, etc. It also analyzes the patterns that deviate from expected norms.
Data Mining - Tasks
Data mining deals with the kind of patterns that can be mined. On the basis of the kind of data to be mined, there are two categories of functions involved in Data Mining −
- Descriptive
- Classification and Prediction
Descriptive Function
The descriptive function deals with the general properties of data in the database. Here is the list of descriptive functions −
- Class/Concept Description
- Mining of Frequent Patterns
- Mining of Associations
- Mining of Correlations
- Mining of Clusters
Class/Concept Description
Class/Concept refers to the data to be associated with the classes or concepts. For example, in a company, the classes of items for sales include computer and printers, and concepts of customers include big spenders and budget spenders. Such descriptions of a class or a concept are called class/concept descriptions. These descriptions can be derived by the following two ways −
Data Characterization − This refers to summarizing data of class under study. This class under study is called as Target Class.
Data Discrimination − It refers to the mapping or classification of a class with some predefined group or class.
Mining of Frequent Patterns
Frequent patterns are those patterns that occur frequently in transactional data. Here is the list of kind of frequent patterns −
Frequent Item Set − It refers to a set of items that frequently appear together, for example, milk and bread.
Frequent Subsequence − A sequence of patterns that occur frequently such as purchasing a camera is followed by memory card.
Frequent Sub Structure − Substructure refers to different structural forms, such as graphs, trees, or lattices, which may be combined with item-sets or subsequences.
Mining of Association
Associations are used in retail sales to identify patterns that are frequently purchased together. This process refers to the process of uncovering the relationship among data and determining association rules.
For example, a retailer generates an association rule that shows that 70% of time milk is sold with bread and only 30% of times biscuits are sold with bread.
Mining of Correlations
It is a kind of additional analysis performed to uncover interesting statistical correlations between associated-attribute-value pairs or between two item sets to analyze that if they have positive, negative or no effect on each other.
Mining of Clusters
Cluster refers to a group of similar kind of objects. Cluster analysis refers to forming group of objects that are very similar to each other but are highly different from the objects in other clusters.
Classification and Prediction
Classification is the process of finding a model that describes the data classes or concepts. The purpose is to be able to use this model to predict the class of objects whose class label is unknown. This derived model is based on the analysis of sets of training data. The derived model can be presented in the following forms −
- Classification (IF-THEN) Rules
- Decision Trees
- Mathematical Formulae
- Neural Networks
The list of functions involved in these processes are as follows −
Classification − It predicts the class of objects whose class label is unknown. Its objective is to find a derived model that describes and distinguishes data classes or concepts. The Derived Model is based on the analysis set of training data i.e. the data object whose class label is well known.
Prediction − It is used to predict missing or unavailable numerical data values rather than class labels. Regression Analysis is generally used for prediction. Prediction can also be used for identification of distribution trends based on available data.
Outlier Analysis − Outliers may be defined as the data objects that do not comply with the general behavior or model of the data available.
Evolution Analysis − Evolution analysis refers to the description and model regularities or trends for objects whose behavior changes over time.
Data Mining Task Primitives
- We can specify a data mining task in the form of a data mining query.
- This query is input to the system.
- A data mining query is defined in terms of data mining task primitives.
Note − These primitives allow us to communicate in an interactive manner with the data mining system. Here is the list of Data Mining Task Primitives −
- Set of task relevant data to be mined.
- Kind of knowledge to be mined.
- Background knowledge to be used in discovery process.
- Interestingness measures and thresholds for pattern evaluation.
- Representation for visualizing the discovered patterns.
Set of task relevant data to be mined
This is the portion of database in which the user is interested. This portion includes the following −
- Database Attributes
- Data Warehouse dimensions of interest
Kind of knowledge to be mined
It refers to the kind of functions to be performed. These functions are −
- Characterization
- Discrimination
- Association and Correlation Analysis
- Classification
- Prediction
- Clustering
- Outlier Analysis
- Evolution Analysis
Background knowledge
The background knowledge allows data to be mined at multiple levels of abstraction. For example, the Concept hierarchies are one of the background knowledge that allows data to be mined at multiple levels of abstraction.
Interestingness measures and thresholds for pattern evaluation
This is used to evaluate the patterns that are discovered by the process of knowledge discovery. There are different interesting measures for different kind of knowledge.
Representation for visualizing the discovered patterns
This refers to the form in which discovered patterns are to be displayed. These representations may include the following. −
- Rules
- Tables
- Charts
- Graphs
- Decision Trees
- Cubes
Data Mining - Issues
Data mining is not an easy task, as the algorithms used can get very complex and data is not always available at one place. It needs to be integrated from various heterogeneous data sources. These factors also create some issues. Here in this tutorial, we will discuss the major issues regarding −
- Mining Methodology and User Interaction
- Performance Issues
- Diverse Data Types Issues
The following diagram describes the major issues.
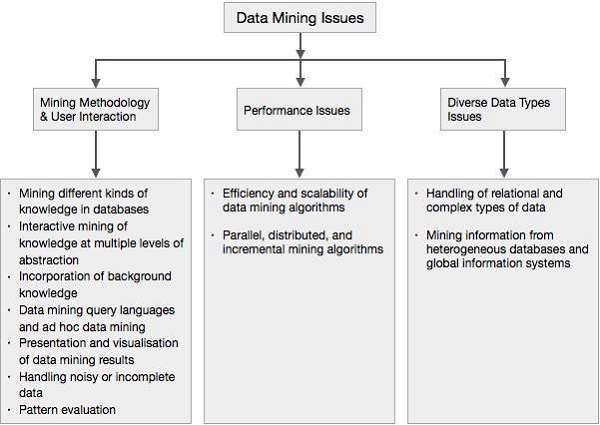
Mining Methodology and User Interaction Issues
It refers to the following kinds of issues −
Mining different kinds of knowledge in databases − Different users may be interested in different kinds of knowledge. Therefore it is necessary for data mining to cover a broad range of knowledge discovery task.
Interactive mining of knowledge at multiple levels of abstraction − The data mining process needs to be interactive because it allows users to focus the search for patterns, providing and refining data mining requests based on the returned results.
Incorporation of background knowledge − To guide discovery process and to express the discovered patterns, the background knowledge can be used. Background knowledge may be used to express the discovered patterns not only in concise terms but at multiple levels of abstraction.
Data mining query languages and ad hoc data mining − Data Mining Query language that allows the user to describe ad hoc mining tasks, should be integrated with a data warehouse query language and optimized for efficient and flexible data mining.
Presentation and visualization of data mining results − Once the patterns are discovered it needs to be expressed in high level languages, and visual representations. These representations should be easily understandable.
Handling noisy or incomplete data − The data cleaning methods are required to handle the noise and incomplete objects while mining the data regularities. If the data cleaning methods are not there then the accuracy of the discovered patterns will be poor.
Pattern evaluation − The patterns discovered should be interesting because either they represent common knowledge or lack novelty.
Performance Issues
There can be performance-related issues such as follows −
Efficiency and scalability of data mining algorithms − In order to effectively extract the information from huge amount of data in databases, data mining algorithm must be efficient and scalable.
Parallel, distributed, and incremental mining algorithms − The factors such as huge size of databases, wide distribution of data, and complexity of data mining methods motivate the development of parallel and distributed data mining algorithms. These algorithms divide the data into partitions which is further processed in a parallel fashion. Then the results from the partitions is merged. The incremental algorithms, update databases without mining the data again from scratch.
Diverse Data Types Issues
Handling of relational and complex types of data − The database may contain complex data objects, multimedia data objects, spatial data, temporal data etc. It is not possible for one system to mine all these kind of data.
Mining information from heterogeneous databases and global information systems − The data is available at different data sources on LAN or WAN. These data source may be structured, semi structured or unstructured. Therefore mining the knowledge from them adds challenges to data mining.
Data Mining - Evaluation
Data Warehouse
A data warehouse exhibits the following characteristics to support the management's decision-making process −
Subject Oriented − Data warehouse is subject oriented because it provides us the information around a subject rather than the organization's ongoing operations. These subjects can be product, customers, suppliers, sales, revenue, etc. The data warehouse does not focus on the ongoing operations, rather it focuses on modelling and analysis of data for decision-making.
Integrated − Data warehouse is constructed by integration of data from heterogeneous sources such as relational databases, flat files etc. This integration enhances the effective analysis of data.
Time Variant − The data collected in a data warehouse is identified with a particular time period. The data in a data warehouse provides information from a historical point of view.
Non-volatile − Nonvolatile means the previous data is not removed when new data is added to it. The data warehouse is kept separate from the operational database therefore frequent changes in operational database is not reflected in the data warehouse.
Data Warehousing
Data warehousing is the process of constructing and using the data warehouse. A data warehouse is constructed by integrating the data from multiple heterogeneous sources. It supports analytical reporting, structured and/or ad hoc queries, and decision making.
Data warehousing involves data cleaning, data integration, and data consolidations. To integrate heterogeneous databases, we have the following two approaches −
- Query Driven Approach
- Update Driven Approach
Query-Driven Approach
This is the traditional approach to integrate heterogeneous databases. This approach is used to build wrappers and integrators on top of multiple heterogeneous databases. These integrators are also known as mediators.
Process of Query Driven Approach
When a query is issued to a client side, a metadata dictionary translates the query into the queries, appropriate for the individual heterogeneous site involved.
Now these queries are mapped and sent to the local query processor.
The results from heterogeneous sites are integrated into a global answer set.
Disadvantages
This approach has the following disadvantages −
The Query Driven Approach needs complex integration and filtering processes.
It is very inefficient and very expensive for frequent queries.
This approach is expensive for queries that require aggregations.
Update-Driven Approach
Today's data warehouse systems follow update-driven approach rather than the traditional approach discussed earlier. In the update-driven approach, the information from multiple heterogeneous sources is integrated in advance and stored in a warehouse. This information is available for direct querying and analysis.
Advantages
This approach has the following advantages −
This approach provides high performance.
The data can be copied, processed, integrated, annotated, summarized and restructured in the semantic data store in advance.
Query processing does not require interface with the processing at local sources.
From Data Warehousing (OLAP) to Data Mining (OLAM)
Online Analytical Mining integrates with Online Analytical Processing with data mining and mining knowledge in multidimensional databases. Here is the diagram that shows the integration of both OLAP and OLAM −
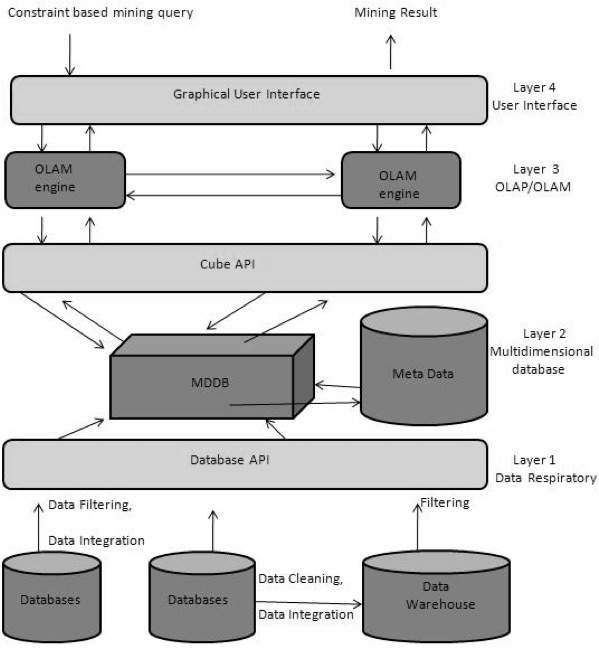
Importance of OLAM
OLAM is important for the following reasons −
High quality of data in data warehouses − The data mining tools are required to work on integrated, consistent, and cleaned data. These steps are very costly in the preprocessing of data. The data warehouses constructed by such preprocessing are valuable sources of high quality data for OLAP and data mining as well.
Available information processing infrastructure surrounding data warehouses − Information processing infrastructure refers to accessing, integration, consolidation, and transformation of multiple heterogeneous databases, web-accessing and service facilities, reporting and OLAP analysis tools.
OLAP−based exploratory data analysis − Exploratory data analysis is required for effective data mining. OLAM provides facility for data mining on various subset of data and at different levels of abstraction.
Online selection of data mining functions − Integrating OLAP with multiple data mining functions and online analytical mining provide users with the flexibility to select desired data mining functions and swap data mining tasks dynamically.
Data Mining - Terminologies
Data Mining
Data mining is defined as extracting the information from a huge set of data. In other words we can say that data mining is mining the knowledge from data. This information can be used for any of the following applications −
- Market Analysis
- Fraud Detection
- Customer Retention
- Production Control
- Science Exploration
Data Mining Engine
Data mining engine is very essential to the data mining system. It consists of a set of functional modules that perform the following functions −
- Characterization
- Association and Correlation Analysis
- Classification
- Prediction
- Cluster analysis
- Outlier analysis
- Evolution analysis
Knowledge Base
This is the domain knowledge. This knowledge is used to guide the search or evaluate the interestingness of the resulting patterns.
Knowledge Discovery
Some people treat data mining same as knowledge discovery, while others view data mining as an essential step in the process of knowledge discovery. Here is the list of steps involved in the knowledge discovery process −
- Data Cleaning
- Data Integration
- Data Selection
- Data Transformation
- Data Mining
- Pattern Evaluation
- Knowledge Presentation
User interface
User interface is the module of data mining system that helps the communication between users and the data mining system. User Interface allows the following functionalities −
- Interact with the system by specifying a data mining query task.
- Providing information to help focus the search.
- Mining based on the intermediate data mining results.
- Browse database and data warehouse schemas or data structures.
- Evaluate mined patterns.
- Visualize the patterns in different forms.
Data Integration
Data Integration is a data preprocessing technique that merges the data from multiple heterogeneous data sources into a coherent data store. Data integration may involve inconsistent data and therefore needs data cleaning.
Data Cleaning
Data cleaning is a technique that is applied to remove the noisy data and correct the inconsistencies in data. Data cleaning involves transformations to correct the wrong data. Data cleaning is performed as a data preprocessing step while preparing the data for a data warehouse.
Data Selection
Data Selection is the process where data relevant to the analysis task are retrieved from the database. Sometimes data transformation and consolidation are performed before the data selection process.
Clusters
Cluster refers to a group of similar kind of objects. Cluster analysis refers to forming group of objects that are very similar to each other but are highly different from the objects in other clusters.
Data Transformation
In this step, data is transformed or consolidated into forms appropriate for mining, by performing summary or aggregation operations.
Data Mining - Knowledge Discovery
What is Knowledge Discovery?
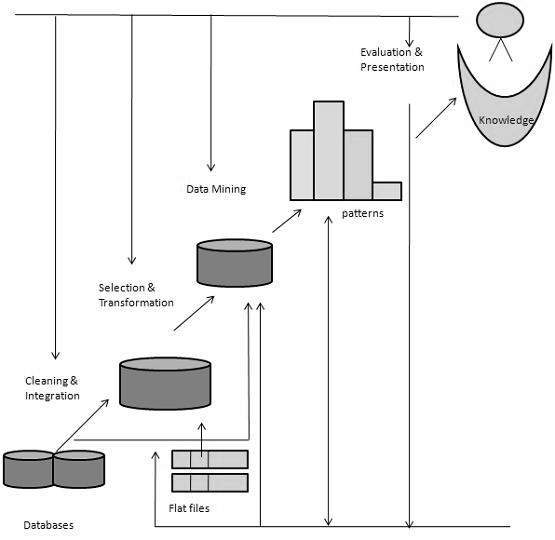
Some people dont differentiate data mining from knowledge discovery while others view data mining as an essential step in the process of knowledge discovery. Here is the list of steps involved in the knowledge discovery process −
Data Cleaning − In this step, the noise and inconsistent data is removed.
Data Integration − In this step, multiple data sources are combined.
Data Selection − In this step, data relevant to the analysis task are retrieved from the database.
Data Transformation − In this step, data is transformed or consolidated into forms appropriate for mining by performing summary or aggregation operations.
Data Mining − In this step, intelligent methods are applied in order to extract data patterns.
Pattern Evaluation − In this step, data patterns are evaluated.
Knowledge Presentation − In this step, knowledge is represented.
The following diagram shows the process of knowledge discovery −
Data Mining - Systems
There is a large variety of data mining systems available. Data mining systems may integrate techniques from the following −
- Spatial Data Analysis
- Information Retrieval
- Pattern Recognition
- Image Analysis
- Signal Processing
- Computer Graphics
- Web Technology
- Business
- Bioinformatics
Data Mining System Classification
A data mining system can be classified according to the following criteria −
- Database Technology
- Statistics
- Machine Learning
- Information Science
- Visualization
- Other Disciplines
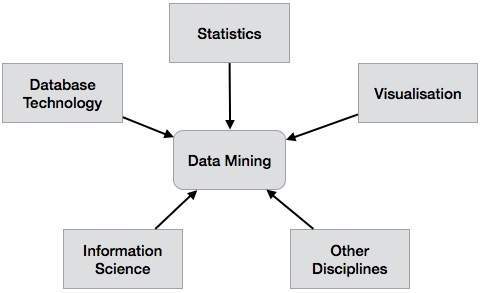
Apart from these, a data mining system can also be classified based on the kind of (a) databases mined, (b) knowledge mined, (c) techniques utilized, and (d) applications adapted.
Classification Based on the Databases Mined
We can classify a data mining system according to the kind of databases mined. Database system can be classified according to different criteria such as data models, types of data, etc. And the data mining system can be classified accordingly.
For example, if we classify a database according to the data model, then we may have a relational, transactional, object-relational, or data warehouse mining system.
Classification Based on the kind of Knowledge Mined
We can classify a data mining system according to the kind of knowledge mined. It means the data mining system is classified on the basis of functionalities such as −
- Characterization
- Discrimination
- Association and Correlation Analysis
- Classification
- Prediction
- Outlier Analysis
- Evolution Analysis
Classification Based on the Techniques Utilized
We can classify a data mining system according to the kind of techniques used. We can describe these techniques according to the degree of user interaction involved or the methods of analysis employed.
Classification Based on the Applications Adapted
We can classify a data mining system according to the applications adapted. These applications are as follows −
- Finance
- Telecommunications
- DNA
- Stock Markets
Integrating a Data Mining System with a DB/DW System
If a data mining system is not integrated with a database or a data warehouse system, then there will be no system to communicate with. This scheme is known as the non-coupling scheme. In this scheme, the main focus is on data mining design and on developing efficient and effective algorithms for mining the available data sets.
The list of Integration Schemes is as follows −
No Coupling − In this scheme, the data mining system does not utilize any of the database or data warehouse functions. It fetches the data from a particular source and processes that data using some data mining algorithms. The data mining result is stored in another file.
Loose Coupling − In this scheme, the data mining system may use some of the functions of database and data warehouse system. It fetches the data from the data respiratory managed by these systems and performs data mining on that data. It then stores the mining result either in a file or in a designated place in a database or in a data warehouse.
Semi−tight Coupling − In this scheme, the data mining system is linked with a database or a data warehouse system and in addition to that, efficient implementations of a few data mining primitives can be provided in the database.
Tight coupling − In this coupling scheme, the data mining system is smoothly integrated into the database or data warehouse system. The data mining subsystem is treated as one functional component of an information system.
Data Mining - Query Language
The Data Mining Query Language (DMQL) was proposed by Han, Fu, Wang, et al. for the DBMiner data mining system. The Data Mining Query Language is actually based on the Structured Query Language (SQL). Data Mining Query Languages can be designed to support ad hoc and interactive data mining. This DMQL provides commands for specifying primitives. The DMQL can work with databases and data warehouses as well. DMQL can be used to define data mining tasks. Particularly we examine how to define data warehouses and data marts in DMQL.
Syntax for Task-Relevant Data Specification
Here is the syntax of DMQL for specifying task-relevant data −
use database database_name or use data warehouse data_warehouse_name in relevance to att_or_dim_list from relation(s)/cube(s) [where condition] order by order_list group by grouping_list
Syntax for Specifying the Kind of Knowledge
Here we will discuss the syntax for Characterization, Discrimination, Association, Classification, and Prediction.
Characterization
The syntax for characterization is −
mine characteristics [as pattern_name]
analyze {measure(s) }
The analyze clause, specifies aggregate measures, such as count, sum, or count%.
For example −
Description describing customer purchasing habits. mine characteristics as customerPurchasing analyze count%
Discrimination
The syntax for Discrimination is −
mine comparison [as {pattern_name]}
For {target_class } where {t arget_condition }
{versus {contrast_class_i }
where {contrast_condition_i}}
analyze {measure(s) }
For example, a user may define big spenders as customers who purchase items that cost $100 or more on an average; and budget spenders as customers who purchase items at less than $100 on an average. The mining of discriminant descriptions for customers from each of these categories can be specified in the DMQL as −
mine comparison as purchaseGroups for bigSpenders where avg(I.price) ≥$100 versus budgetSpenders where avg(I.price)< $100 analyze count
Association
The syntax for Association is−
mine associations [ as {pattern_name} ]
{matching {metapattern} }
For Example −
mine associations as buyingHabits matching P(X:customer,W) ^ Q(X,Y) ≥ buys(X,Z)
where X is key of customer relation; P and Q are predicate variables; and W, Y, and Z are object variables.
Classification
The syntax for Classification is −
mine classification [as pattern_name] analyze classifying_attribute_or_dimension
For example, to mine patterns, classifying customer credit rating where the classes are determined by the attribute credit_rating, and mine classification is determined as classifyCustomerCreditRating.
analyze credit_rating
Prediction
The syntax for prediction is −
mine prediction [as pattern_name]
analyze prediction_attribute_or_dimension
{set {attribute_or_dimension_i= value_i}}
Syntax for Concept Hierarchy Specification
To specify concept hierarchies, use the following syntax −
use hierarchy <hierarchy> for <attribute_or_dimension>
We use different syntaxes to define different types of hierarchies such as−
-schema hierarchies
define hierarchy time_hierarchy on date as [date,month quarter,year]
-
set-grouping hierarchies
define hierarchy age_hierarchy for age on customer as
level1: {young, middle_aged, senior} < level0: all
level2: {20, ..., 39} < level1: young
level3: {40, ..., 59} < level1: middle_aged
level4: {60, ..., 89} < level1: senior
-operation-derived hierarchies
define hierarchy age_hierarchy for age on customer as
{age_category(1), ..., age_category(5)}
:= cluster(default, age, 5) < all(age)
-rule-based hierarchies
define hierarchy profit_margin_hierarchy on item as
level_1: low_profit_margin < level_0: all
if (price - cost)< $50
level_1: medium-profit_margin < level_0: all
if ((price - cost) > $50) and ((price - cost) ≤ $250))
level_1: high_profit_margin < level_0: all
Syntax for Interestingness Measures Specification
Interestingness measures and thresholds can be specified by the user with the statement −
with <interest_measure_name> threshold = threshold_value
For Example −
with support threshold = 0.05 with confidence threshold = 0.7
Syntax for Pattern Presentation and Visualization Specification
We have a syntax, which allows users to specify the display of discovered patterns in one or more forms.
display as <result_form>
For Example −
display as table
Full Specification of DMQL
As a market manager of a company, you would like to characterize the buying habits of customers who can purchase items priced at no less than $100; with respect to the customer's age, type of item purchased, and the place where the item was purchased. You would like to know the percentage of customers having that characteristic. In particular, you are only interested in purchases made in Canada, and paid with an American Express credit card. You would like to view the resulting descriptions in the form of a table.
use database AllElectronics_db use hierarchy location_hierarchy for B.address mine characteristics as customerPurchasing analyze count% in relevance to C.age,I.type,I.place_made from customer C, item I, purchase P, items_sold S, branch B where I.item_ID = S.item_ID and P.cust_ID = C.cust_ID and P.method_paid = "AmEx" and B.address = "Canada" and I.price ≥ 100 with noise threshold = 5% display as table
Data Mining Languages Standardization
Standardizing the Data Mining Languages will serve the following purposes −
Helps systematic development of data mining solutions.
Improves interoperability among multiple data mining systems and functions.
Promotes education and rapid learning.
Promotes the use of data mining systems in industry and society.
Data Mining - Classification & Prediction
There are two forms of data analysis that can be used for extracting models describing important classes or to predict future data trends. These two forms are as follows −
- Classification
- Prediction
Classification models predict categorical class labels; and prediction models predict continuous valued functions. For example, we can build a classification model to categorize bank loan applications as either safe or risky, or a prediction model to predict the expenditures in dollars of potential customers on computer equipment given their income and occupation.
What is classification?
Following are the examples of cases where the data analysis task is Classification −
A bank loan officer wants to analyze the data in order to know which customer (loan applicant) are risky or which are safe.
A marketing manager at a company needs to analyze a customer with a given profile, who will buy a new computer.
In both of the above examples, a model or classifier is constructed to predict the categorical labels. These labels are risky or safe for loan application data and yes or no for marketing data.
What is prediction?
Following are the examples of cases where the data analysis task is Prediction −
Suppose the marketing manager needs to predict how much a given customer will spend during a sale at his company. In this example we are bothered to predict a numeric value. Therefore the data analysis task is an example of numeric prediction. In this case, a model or a predictor will be constructed that predicts a continuous-valued-function or ordered value.
Note − Regression analysis is a statistical methodology that is most often used for numeric prediction.
How Does Classification Works?
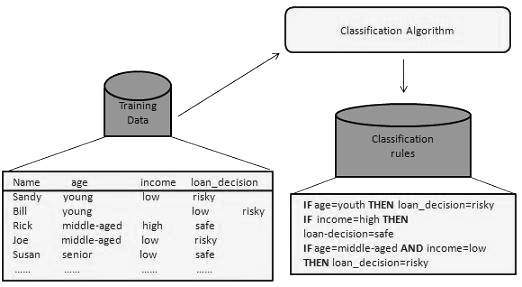
With the help of the bank loan application that we have discussed above, let us understand the working of classification. The Data Classification process includes two steps −
- Building the Classifier or Model
- Using Classifier for Classification
Building the Classifier or Model
This step is the learning step or the learning phase.
In this step the classification algorithms build the classifier.
The classifier is built from the training set made up of database tuples and their associated class labels.
Each tuple that constitutes the training set is referred to as a category or class. These tuples can also be referred to as sample, object or data points.
Using Classifier for Classification
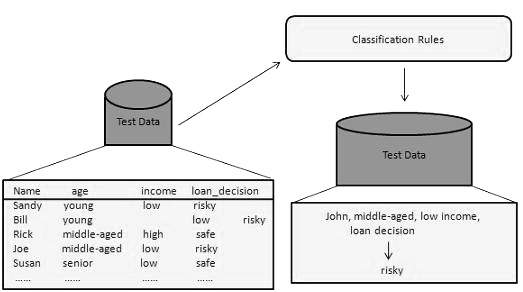
In this step, the classifier is used for classification. Here the test data is used to estimate the accuracy of classification rules. The classification rules can be applied to the new data tuples if the accuracy is considered acceptable.
Classification and Prediction Issues
The major issue is preparing the data for Classification and Prediction. Preparing the data involves the following activities −
Data Cleaning − Data cleaning involves removing the noise and treatment of missing values. The noise is removed by applying smoothing techniques and the problem of missing values is solved by replacing a missing value with most commonly occurring value for that attribute.
Relevance Analysis − Database may also have the irrelevant attributes. Correlation analysis is used to know whether any two given attributes are related.
-
Data Transformation and reduction − The data can be transformed by any of the following methods.
Normalization − The data is transformed using normalization. Normalization involves scaling all values for given attribute in order to make them fall within a small specified range. Normalization is used when in the learning step, the neural networks or the methods involving measurements are used.
Generalization − The data can also be transformed by generalizing it to the higher concept. For this purpose we can use the concept hierarchies.
Note − Data can also be reduced by some other methods such as wavelet transformation, binning, histogram analysis, and clustering.
Comparison of Classification and Prediction Methods
Here is the criteria for comparing the methods of Classification and Prediction −
Accuracy − Accuracy of classifier refers to the ability of classifier. It predict the class label correctly and the accuracy of the predictor refers to how well a given predictor can guess the value of predicted attribute for a new data.
Speed − This refers to the computational cost in generating and using the classifier or predictor.
Robustness − It refers to the ability of classifier or predictor to make correct predictions from given noisy data.
Scalability − Scalability refers to the ability to construct the classifier or predictor efficiently; given large amount of data.
Interpretability − It refers to what extent the classifier or predictor understands.
Data Mining - Decision Tree Induction
A decision tree is a structure that includes a root node, branches, and leaf nodes. Each internal node denotes a test on an attribute, each branch denotes the outcome of a test, and each leaf node holds a class label. The topmost node in the tree is the root node.
The following decision tree is for the concept buy_computer that indicates whether a customer at a company is likely to buy a computer or not. Each internal node represents a test on an attribute. Each leaf node represents a class.
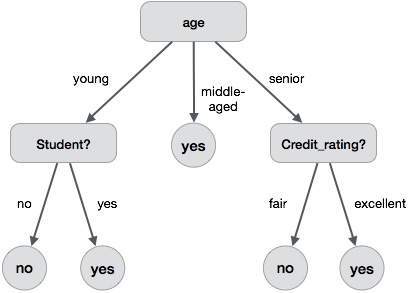
The benefits of having a decision tree are as follows −
- It does not require any domain knowledge.
- It is easy to comprehend.
- The learning and classification steps of a decision tree are simple and fast.
Decision Tree Induction Algorithm
A machine researcher named J. Ross Quinlan in 1980 developed a decision tree algorithm known as ID3 (Iterative Dichotomiser). Later, he presented C4.5, which was the successor of ID3. ID3 and C4.5 adopt a greedy approach. In this algorithm, there is no backtracking; the trees are constructed in a top-down recursive divide-and-conquer manner.
Generating a decision tree form training tuples of data partition D
Algorithm : Generate_decision_tree
Input:
Data partition, D, which is a set of training tuples
and their associated class labels.
attribute_list, the set of candidate attributes.
Attribute selection method, a procedure to determine the
splitting criterion that best partitions that the data
tuples into individual classes. This criterion includes a
splitting_attribute and either a splitting point or splitting subset.
Output:
A Decision Tree
Method
create a node N;
if tuples in D are all of the same class, C then
return N as leaf node labeled with class C;
if attribute_list is empty then
return N as leaf node with labeled
with majority class in D;|| majority voting
apply attribute_selection_method(D, attribute_list)
to find the best splitting_criterion;
label node N with splitting_criterion;
if splitting_attribute is discrete-valued and
multiway splits allowed then // no restricted to binary trees
attribute_list = splitting attribute; // remove splitting attribute
for each outcome j of splitting criterion
// partition the tuples and grow subtrees for each partition
let Dj be the set of data tuples in D satisfying outcome j; // a partition
if Dj is empty then
attach a leaf labeled with the majority
class in D to node N;
else
attach the node returned by Generate
decision tree(Dj, attribute list) to node N;
end for
return N;
Tree Pruning
Tree pruning is performed in order to remove anomalies in the training data due to noise or outliers. The pruned trees are smaller and less complex.
Tree Pruning Approaches
There are two approaches to prune a tree −
Pre-pruning − The tree is pruned by halting its construction early.
Post-pruning - This approach removes a sub-tree from a fully grown tree.
Cost Complexity
The cost complexity is measured by the following two parameters −
- Number of leaves in the tree, and
- Error rate of the tree.
Data Mining - Bayesian Classification
Bayesian classification is based on Bayes' Theorem. Bayesian classifiers are the statistical classifiers. Bayesian classifiers can predict class membership probabilities such as the probability that a given tuple belongs to a particular class.
Baye's Theorem
Bayes' Theorem is named after Thomas Bayes. There are two types of probabilities −
- Posterior Probability [P(H/X)]
- Prior Probability [P(H)]
where X is data tuple and H is some hypothesis.
According to Bayes' Theorem,
Bayesian Belief Network
Bayesian Belief Networks specify joint conditional probability distributions. They are also known as Belief Networks, Bayesian Networks, or Probabilistic Networks.
A Belief Network allows class conditional independencies to be defined between subsets of variables.
It provides a graphical model of causal relationship on which learning can be performed.
We can use a trained Bayesian Network for classification.
There are two components that define a Bayesian Belief Network −
- Directed acyclic graph
- A set of conditional probability tables
Directed Acyclic Graph
- Each node in a directed acyclic graph represents a random variable.
- These variable may be discrete or continuous valued.
- These variables may correspond to the actual attribute given in the data.
Directed Acyclic Graph Representation
The following diagram shows a directed acyclic graph for six Boolean variables.
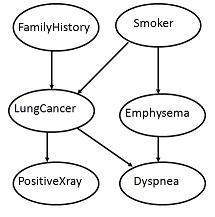
The arc in the diagram allows representation of causal knowledge. For example, lung cancer is influenced by a person's family history of lung cancer, as well as whether or not the person is a smoker. It is worth noting that the variable PositiveXray is independent of whether the patient has a family history of lung cancer or that the patient is a smoker, given that we know the patient has lung cancer.
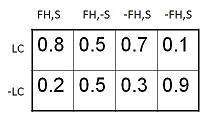
Conditional Probability Table
The conditional probability table for the values of the variable LungCancer (LC) showing each possible combination of the values of its parent nodes, FamilyHistory (FH), and Smoker (S) is as follows −
Data Mining - Rule Based Classification
IF-THEN Rules
Rule-based classifier makes use of a set of IF-THEN rules for classification. We can express a rule in the following from −
Let us consider a rule R1,
R1: IF age = youth AND student = yes THEN buy_computer = yes
Points to remember −
The IF part of the rule is called rule antecedent or precondition.
The THEN part of the rule is called rule consequent.
The antecedent part the condition consist of one or more attribute tests and these tests are logically ANDed.
The consequent part consists of class prediction.
Note − We can also write rule R1 as follows −
R1: (age = youth) ^ (student = yes))(buys computer = yes)
If the condition holds true for a given tuple, then the antecedent is satisfied.
Rule Extraction
Here we will learn how to build a rule-based classifier by extracting IF-THEN rules from a decision tree.
Points to remember −
To extract a rule from a decision tree −
One rule is created for each path from the root to the leaf node.
To form a rule antecedent, each splitting criterion is logically ANDed.
The leaf node holds the class prediction, forming the rule consequent.
Rule Induction Using Sequential Covering Algorithm
Sequential Covering Algorithm can be used to extract IF-THEN rules form the training data. We do not require to generate a decision tree first. In this algorithm, each rule for a given class covers many of the tuples of that class.
Some of the sequential Covering Algorithms are AQ, CN2, and RIPPER. As per the general strategy the rules are learned one at a time. For each time rules are learned, a tuple covered by the rule is removed and the process continues for the rest of the tuples. This is because the path to each leaf in a decision tree corresponds to a rule.
Note − The Decision tree induction can be considered as learning a set of rules simultaneously.
The Following is the sequential learning Algorithm where rules are learned for one class at a time. When learning a rule from a class Ci, we want the rule to cover all the tuples from class C only and no tuple form any other class.
Algorithm: Sequential Covering
Input:
D, a data set class-labeled tuples,
Att_vals, the set of all attributes and their possible values.
Output: A Set of IF-THEN rules.
Method:
Rule_set={ }; // initial set of rules learned is empty
for each class c do
repeat
Rule = Learn_One_Rule(D, Att_valls, c);
remove tuples covered by Rule form D;
until termination condition;
Rule_set=Rule_set+Rule; // add a new rule to rule-set
end for
return Rule_Set;
Rule Pruning
The rule is pruned is due to the following reason −
The Assessment of quality is made on the original set of training data. The rule may perform well on training data but less well on subsequent data. That's why the rule pruning is required.
The rule is pruned by removing conjunct. The rule R is pruned, if pruned version of R has greater quality than what was assessed on an independent set of tuples.
FOIL is one of the simple and effective method for rule pruning. For a given rule R,
where pos and neg is the number of positive tuples covered by R, respectively.
Note − This value will increase with the accuracy of R on the pruning set. Hence, if the FOIL_Prune value is higher for the pruned version of R, then we prune R.
Miscellaneous Classification Methods
Here we will discuss other classification methods such as Genetic Algorithms, Rough Set Approach, and Fuzzy Set Approach.
Genetic Algorithms
The idea of genetic algorithm is derived from natural evolution. In genetic algorithm, first of all, the initial population is created. This initial population consists of randomly generated rules. We can represent each rule by a string of bits.
For example, in a given training set, the samples are described by two Boolean attributes such as A1 and A2. And this given training set contains two classes such as C1 and C2.
We can encode the rule IF A1 AND NOT A2 THEN C2 into a bit string 100. In this bit representation, the two leftmost bits represent the attribute A1 and A2, respectively.
Likewise, the rule IF NOT A1 AND NOT A2 THEN C1 can be encoded as 001.
Note − If the attribute has K values where K>2, then we can use the K bits to encode the attribute values. The classes are also encoded in the same manner.
Points to remember −
Based on the notion of the survival of the fittest, a new population is formed that consists of the fittest rules in the current population and offspring values of these rules as well.
The fitness of a rule is assessed by its classification accuracy on a set of training samples.
The genetic operators such as crossover and mutation are applied to create offspring.
In crossover, the substring from pair of rules are swapped to form a new pair of rules.
In mutation, randomly selected bits in a rule's string are inverted.
Rough Set Approach
We can use the rough set approach to discover structural relationship within imprecise and noisy data.
Note − This approach can only be applied on discrete-valued attributes. Therefore, continuous-valued attributes must be discretized before its use.
The Rough Set Theory is based on the establishment of equivalence classes within the given training data. The tuples that forms the equivalence class are indiscernible. It means the samples are identical with respect to the attributes describing the data.
There are some classes in the given real world data, which cannot be distinguished in terms of available attributes. We can use the rough sets to roughly define such classes.
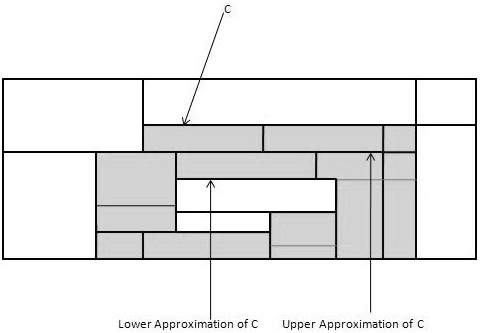
For a given class C, the rough set definition is approximated by two sets as follows −
Lower Approximation of C − The lower approximation of C consists of all the data tuples, that based on the knowledge of the attribute, are certain to belong to class C.
Upper Approximation of C − The upper approximation of C consists of all the tuples, that based on the knowledge of attributes, cannot be described as not belonging to C.
The following diagram shows the Upper and Lower Approximation of class C −
Fuzzy Set Approaches
Fuzzy Set Theory is also called Possibility Theory. This theory was proposed by Lotfi Zadeh in 1965 as an alternative the two-value logic and probability theory. This theory allows us to work at a high level of abstraction. It also provides us the means for dealing with imprecise measurement of data.
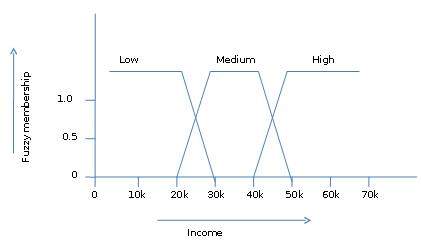
The fuzzy set theory also allows us to deal with vague or inexact facts. For example, being a member of a set of high incomes is in exact (e.g. if $50,000 is high then what about $49,000 and $48,000). Unlike the traditional CRISP set where the element either belong to S or its complement but in fuzzy set theory the element can belong to more than one fuzzy set.
For example, the income value $49,000 belongs to both the medium and high fuzzy sets but to differing degrees. Fuzzy set notation for this income value is as follows −
mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96
where m is the membership function that operates on the fuzzy sets of medium_income and high_income respectively. This notation can be shown diagrammatically as follows −
Data Mining - Cluster Analysis
Cluster is a group of objects that belongs to the same class. In other words, similar objects are grouped in one cluster and dissimilar objects are grouped in another cluster.
What is Clustering?
Clustering is the process of making a group of abstract objects into classes of similar objects.
Points to Remember
A cluster of data objects can be treated as one group.
While doing cluster analysis, we first partition the set of data into groups based on data similarity and then assign the labels to the groups.
The main advantage of clustering over classification is that, it is adaptable to changes and helps single out useful features that distinguish different groups.
Applications of Cluster Analysis
Clustering analysis is broadly used in many applications such as market research, pattern recognition, data analysis, and image processing.
Clustering can also help marketers discover distinct groups in their customer base. And they can characterize their customer groups based on the purchasing patterns.
In the field of biology, it can be used to derive plant and animal taxonomies, categorize genes with similar functionalities and gain insight into structures inherent to populations.
Clustering also helps in identification of areas of similar land use in an earth observation database. It also helps in the identification of groups of houses in a city according to house type, value, and geographic location.
Clustering also helps in classifying documents on the web for information discovery.
Clustering is also used in outlier detection applications such as detection of credit card fraud.
As a data mining function, cluster analysis serves as a tool to gain insight into the distribution of data to observe characteristics of each cluster.
Requirements of Clustering in Data Mining
The following points throw light on why clustering is required in data mining −
Scalability − We need highly scalable clustering algorithms to deal with large databases.
Ability to deal with different kinds of attributes − Algorithms should be capable to be applied on any kind of data such as interval-based (numerical) data, categorical, and binary data.
Discovery of clusters with attribute shape − The clustering algorithm should be capable of detecting clusters of arbitrary shape. They should not be bounded to only distance measures that tend to find spherical cluster of small sizes.
High dimensionality − The clustering algorithm should not only be able to handle low-dimensional data but also the high dimensional space.
Ability to deal with noisy data − Databases contain noisy, missing or erroneous data. Some algorithms are sensitive to such data and may lead to poor quality clusters.
Interpretability − The clustering results should be interpretable, comprehensible, and usable.
Clustering Methods
Clustering methods can be classified into the following categories −
- Partitioning Method
- Hierarchical Method
- Density-based Method
- Grid-Based Method
- Model-Based Method
- Constraint-based Method
Partitioning Method
Suppose we are given a database of n objects and the partitioning method constructs k partition of data. Each partition will represent a cluster and k ≤ n. It means that it will classify the data into k groups, which satisfy the following requirements −
Each group contains at least one object.
Each object must belong to exactly one group.
Points to remember −
For a given number of partitions (say k), the partitioning method will create an initial partitioning.
Then it uses the iterative relocation technique to improve the partitioning by moving objects from one group to other.
Hierarchical Methods
This method creates a hierarchical decomposition of the given set of data objects. We can classify hierarchical methods on the basis of how the hierarchical decomposition is formed. There are two approaches here −
- Agglomerative Approach
- Divisive Approach
Agglomerative Approach
This approach is also known as the bottom-up approach. In this, we start with each object forming a separate group. It keeps on merging the objects or groups that are close to one another. It keep on doing so until all of the groups are merged into one or until the termination condition holds.
Divisive Approach
This approach is also known as the top-down approach. In this, we start with all of the objects in the same cluster. In the continuous iteration, a cluster is split up into smaller clusters. It is down until each object in one cluster or the termination condition holds. This method is rigid, i.e., once a merging or splitting is done, it can never be undone.
Approaches to Improve Quality of Hierarchical Clustering
Here are the two approaches that are used to improve the quality of hierarchical clustering −
Perform careful analysis of object linkages at each hierarchical partitioning.
Integrate hierarchical agglomeration by first using a hierarchical agglomerative algorithm to group objects into micro-clusters, and then performing macro-clustering on the micro-clusters.
Density-based Method
This method is based on the notion of density. The basic idea is to continue growing the given cluster as long as the density in the neighborhood exceeds some threshold, i.e., for each data point within a given cluster, the radius of a given cluster has to contain at least a minimum number of points.
Grid-based Method
In this, the objects together form a grid. The object space is quantized into finite number of cells that form a grid structure.
Advantages
The major advantage of this method is fast processing time.
It is dependent only on the number of cells in each dimension in the quantized space.
Model-based methods
In this method, a model is hypothesized for each cluster to find the best fit of data for a given model. This method locates the clusters by clustering the density function. It reflects spatial distribution of the data points.
This method also provides a way to automatically determine the number of clusters based on standard statistics, taking outlier or noise into account. It therefore yields robust clustering methods.
Constraint-based Method
In this method, the clustering is performed by the incorporation of user or application-oriented constraints. A constraint refers to the user expectation or the properties of desired clustering results. Constraints provide us with an interactive way of communication with the clustering process. Constraints can be specified by the user or the application requirement.
Data Mining - Mining Text Data
Text databases consist of huge collection of documents. They collect these information from several sources such as news articles, books, digital libraries, e-mail messages, web pages, etc. Due to increase in the amount of information, the text databases are growing rapidly. In many of the text databases, the data is semi-structured.
For example, a document may contain a few structured fields, such as title, author, publishing_date, etc. But along with the structure data, the document also contains unstructured text components, such as abstract and contents. Without knowing what could be in the documents, it is difficult to formulate effective queries for analyzing and extracting useful information from the data. Users require tools to compare the documents and rank their importance and relevance. Therefore, text mining has become popular and an essential theme in data mining.
Information Retrieval
Information retrieval deals with the retrieval of information from a large number of text-based documents. Some of the database systems are not usually present in information retrieval systems because both handle different kinds of data. Examples of information retrieval system include −
- Online Library catalogue system
- Online Document Management Systems
- Web Search Systems etc.
Note − The main problem in an information retrieval system is to locate relevant documents in a document collection based on a user's query. This kind of user's query consists of some keywords describing an information need.
In such search problems, the user takes an initiative to pull relevant information out from a collection. This is appropriate when the user has ad-hoc information need, i.e., a short-term need. But if the user has a long-term information need, then the retrieval system can also take an initiative to push any newly arrived information item to the user.
This kind of access to information is called Information Filtering. And the corresponding systems are known as Filtering Systems or Recommender Systems.
Basic Measures for Text Retrieval
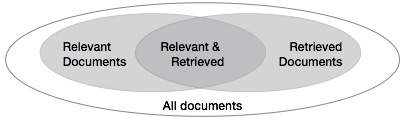
We need to check the accuracy of a system when it retrieves a number of documents on the basis of user's input. Let the set of documents relevant to a query be denoted as {Relevant} and the set of retrieved document as {Retrieved}. The set of documents that are relevant and retrieved can be denoted as {Relevant} {Retrieved}. This can be shown in the form of a Venn diagram as follows −
There are three fundamental measures for assessing the quality of text retrieval −
- Precision
- Recall
- F-score
Precision
Precision is the percentage of retrieved documents that are in fact relevant to the query. Precision can be defined as −
Precision= |{Relevant} ∩ {Retrieved}| / |{Retrieved}|
Recall
Recall is the percentage of documents that are relevant to the query and were in fact retrieved. Recall is defined as −
Recall = |{Relevant} ∩ {Retrieved}| / |{Relevant}|
F-score
F-score is the commonly used trade-off. The information retrieval system often needs to trade-off for precision or vice versa. F-score is defined as harmonic mean of recall or precision as follows −
F-score = recall x precision / (recall + precision) / 2
Data Mining - Mining World Wide Web
The World Wide Web contains huge amounts of information that provides a rich source for data mining.
Challenges in Web Mining
The web poses great challenges for resource and knowledge discovery based on the following observations −
The web is too huge − The size of the web is very huge and rapidly increasing. This seems that the web is too huge for data warehousing and data mining.
Complexity of Web pages − The web pages do not have unifying structure. They are very complex as compared to traditional text document. There are huge amount of documents in digital library of web. These libraries are not arranged according to any particular sorted order.
Web is dynamic information source − The information on the web is rapidly updated. The data such as news, stock markets, weather, sports, shopping, etc., are regularly updated.
Diversity of user communities − The user community on the web is rapidly expanding. These users have different backgrounds, interests, and usage purposes. There are more than 100 million workstations that are connected to the Internet and still rapidly increasing.
Relevancy of Information − It is considered that a particular person is generally interested in only small portion of the web, while the rest of the portion of the web contains the information that is not relevant to the user and may swamp desired results.
Mining Web page layout structure
The basic structure of the web page is based on the Document Object Model (DOM). The DOM structure refers to a tree like structure where the HTML tag in the page corresponds to a node in the DOM tree. We can segment the web page by using predefined tags in HTML. The HTML syntax is flexible therefore, the web pages does not follow the W3C specifications. Not following the specifications of W3C may cause error in DOM tree structure.
The DOM structure was initially introduced for presentation in the browser and not for description of semantic structure of the web page. The DOM structure cannot correctly identify the semantic relationship between the different parts of a web page.
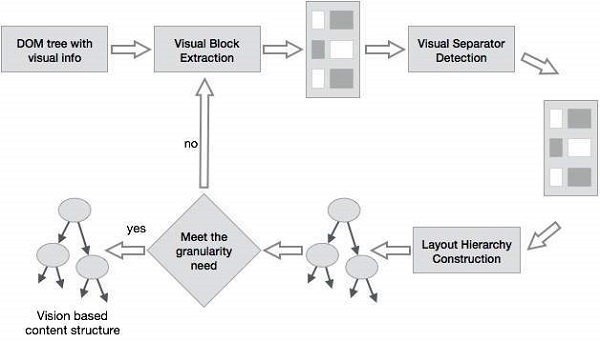
Vision-based page segmentation (VIPS)
The purpose of VIPS is to extract the semantic structure of a web page based on its visual presentation.
Such a semantic structure corresponds to a tree structure. In this tree each node corresponds to a block.
A value is assigned to each node. This value is called the Degree of Coherence. This value is assigned to indicate the coherent content in the block based on visual perception.
The VIPS algorithm first extracts all the suitable blocks from the HTML DOM tree. After that it finds the separators between these blocks.
The separators refer to the horizontal or vertical lines in a web page that visually cross with no blocks.
The semantics of the web page is constructed on the basis of these blocks.
The following figure shows the procedure of VIPS algorithm −
Data Mining - Applications & Trends
Data mining is widely used in diverse areas. There are a number of commercial data mining system available today and yet there are many challenges in this field. In this tutorial, we will discuss the applications and the trend of data mining.
Data Mining Applications
Here is the list of areas where data mining is widely used −
- Financial Data Analysis
- Retail Industry
- Telecommunication Industry
- Biological Data Analysis
- Other Scientific Applications
- Intrusion Detection
Financial Data Analysis
The financial data in banking and financial industry is generally reliable and of high quality which facilitates systematic data analysis and data mining. Some of the typical cases are as follows −
Design and construction of data warehouses for multidimensional data analysis and data mining.
Loan payment prediction and customer credit policy analysis.
Classification and clustering of customers for targeted marketing.
Detection of money laundering and other financial crimes.
Retail Industry
Data Mining has its great application in Retail Industry because it collects large amount of data from on sales, customer purchasing history, goods transportation, consumption and services. It is natural that the quantity of data collected will continue to expand rapidly because of the increasing ease, availability and popularity of the web.
Data mining in retail industry helps in identifying customer buying patterns and trends that lead to improved quality of customer service and good customer retention and satisfaction. Here is the list of examples of data mining in the retail industry −
Design and Construction of data warehouses based on the benefits of data mining.
Multidimensional analysis of sales, customers, products, time and region.
Analysis of effectiveness of sales campaigns.
Customer Retention.
Product recommendation and cross-referencing of items.
Telecommunication Industry
Today the telecommunication industry is one of the most emerging industries providing various services such as fax, pager, cellular phone, internet messenger, images, e-mail, web data transmission, etc. Due to the development of new computer and communication technologies, the telecommunication industry is rapidly expanding. This is the reason why data mining is become very important to help and understand the business.
Data mining in telecommunication industry helps in identifying the telecommunication patterns, catch fraudulent activities, make better use of resource, and improve quality of service. Here is the list of examples for which data mining improves telecommunication services −
Multidimensional Analysis of Telecommunication data.
Fraudulent pattern analysis.
Identification of unusual patterns.
Multidimensional association and sequential patterns analysis.
Mobile Telecommunication services.
Use of visualization tools in telecommunication data analysis.
Biological Data Analysis
In recent times, we have seen a tremendous growth in the field of biology such as genomics, proteomics, functional Genomics and biomedical research. Biological data mining is a very important part of Bioinformatics. Following are the aspects in which data mining contributes for biological data analysis −
Semantic integration of heterogeneous, distributed genomic and proteomic databases.
Alignment, indexing, similarity search and comparative analysis multiple nucleotide sequences.
Discovery of structural patterns and analysis of genetic networks and protein pathways.
Association and path analysis.
Visualization tools in genetic data analysis.
Other Scientific Applications
The applications discussed above tend to handle relatively small and homogeneous data sets for which the statistical techniques are appropriate. Huge amount of data have been collected from scientific domains such as geosciences, astronomy, etc. A large amount of data sets is being generated because of the fast numerical simulations in various fields such as climate and ecosystem modeling, chemical engineering, fluid dynamics, etc. Following are the applications of data mining in the field of Scientific Applications −
- Data Warehouses and data preprocessing.
- Graph-based mining.
- Visualization and domain specific knowledge.
Intrusion Detection
Intrusion refers to any kind of action that threatens integrity, confidentiality, or the availability of network resources. In this world of connectivity, security has become the major issue. With increased usage of internet and availability of the tools and tricks for intruding and attacking network prompted intrusion detection to become a critical component of network administration. Here is the list of areas in which data mining technology may be applied for intrusion detection −
Development of data mining algorithm for intrusion detection.
Association and correlation analysis, aggregation to help select and build discriminating attributes.
Analysis of Stream data.
Distributed data mining.
Visualization and query tools.
Data Mining System Products
There are many data mining system products and domain specific data mining applications. The new data mining systems and applications are being added to the previous systems. Also, efforts are being made to standardize data mining languages.
Choosing a Data Mining System
The selection of a data mining system depends on the following features −
Data Types − The data mining system may handle formatted text, record-based data, and relational data. The data could also be in ASCII text, relational database data or data warehouse data. Therefore, we should check what exact format the data mining system can handle.
System Issues − We must consider the compatibility of a data mining system with different operating systems. One data mining system may run on only one operating system or on several. There are also data mining systems that provide web-based user interfaces and allow XML data as input.
Data Sources − Data sources refer to the data formats in which data mining system will operate. Some data mining system may work only on ASCII text files while others on multiple relational sources. Data mining system should also support ODBC connections or OLE DB for ODBC connections.
Data Mining functions and methodologies − There are some data mining systems that provide only one data mining function such as classification while some provides multiple data mining functions such as concept description, discovery-driven OLAP analysis, association mining, linkage analysis, statistical analysis, classification, prediction, clustering, outlier analysis, similarity search, etc.
-
Coupling data mining with databases or data warehouse systems − Data mining systems need to be coupled with a database or a data warehouse system. The coupled components are integrated into a uniform information processing environment. Here are the types of coupling listed below −
- No coupling
- Loose Coupling
- Semi tight Coupling
- Tight Coupling
-
Scalability − There are two scalability issues in data mining −
Row (Database size) Scalability − A data mining system is considered as row scalable when the number or rows are enlarged 10 times. It takes no more than 10 times to execute a query.
Column (Dimension) Salability − A data mining system is considered as column scalable if the mining query execution time increases linearly with the number of columns.
-
Visualization Tools − Visualization in data mining can be categorized as follows −
- Data Visualization
- Mining Results Visualization
- Mining process visualization
- Visual data mining
Data Mining query language and graphical user interface − An easy-to-use graphical user interface is important to promote user-guided, interactive data mining. Unlike relational database systems, data mining systems do not share underlying data mining query language.
Trends in Data Mining
Data mining concepts are still evolving and here are the latest trends that we get to see in this field −
Application Exploration.
Scalable and interactive data mining methods.
Integration of data mining with database systems, data warehouse systems and web database systems.
SStandardization of data mining query language.
Visual data mining.
New methods for mining complex types of data.
Biological data mining.
Data mining and software engineering.
Web mining.
Distributed data mining.
Real time data mining.
Multi database data mining.
Privacy protection and information security in data mining.
Data Mining - Themes
Theoretical Foundations of Data Mining
The theoretical foundations of data mining includes the following concepts −
-
Data Reduction − The basic idea of this theory is to reduce the data representation which trades accuracy for speed in response to the need to obtain quick approximate answers to queries on very large databases. Some of the data reduction techniques are as follows −
Singular value Decomposition
Wavelets
Regression
Log-linear models
Histograms
Clustering
Sampling
Construction of Index Trees
-
Data Compression − The basic idea of this theory is to compress the given data by encoding in terms of the following −
Bits
Association Rules
Decision Trees
Clusters
-
Pattern Discovery − The basic idea of this theory is to discover patterns occurring in a database. Following are the areas that contribute to this theory −
Machine Learning
Neural Network
Association Mining
Sequential Pattern Matching
Clustering
Probability Theory − This theory is based on statistical theory. The basic idea behind this theory is to discover joint probability distributions of random variables.
Probability Theory − According to this theory, data mining finds the patterns that are interesting only to the extent that they can be used in the decision-making process of some enterprise.
Microeconomic View − As per this theory, a database schema consists of data and patterns that are stored in a database. Therefore, data mining is the task of performing induction on databases.
Inductive databases − Apart from the database-oriented techniques, there are statistical techniques available for data analysis. These techniques can be applied to scientific data and data from economic and social sciences as well.
Statistical Data Mining
Some of the Statistical Data Mining Techniques are as follows −
-
Regression − Regression methods are used to predict the value of the response variable from one or more predictor variables where the variables are numeric. Listed below are the forms of Regression −
Linear
Multiple
Weighted
Polynomial
Nonparametric
Robust
-
Generalized Linear Models − Generalized Linear Model includes −
Logistic Regression
Poisson Regression
The model's generalization allows a categorical response variable to be related to a set of predictor variables in a manner similar to the modelling of numeric response variable using linear regression.
-
Analysis of Variance − This technique analyzes −
Experimental data for two or more populations described by a numeric response variable.
One or more categorical variables (factors).
Mixed-effect Models − These models are used for analyzing grouped data. These models describe the relationship between a response variable and some co-variates in the data grouped according to one or more factors.
Factor Analysis − Factor analysis is used to predict a categorical response variable. This method assumes that independent variables follow a multivariate normal distribution.
-
Time Series Analysis − Following are the methods for analyzing time-series data −
Auto-regression Methods.
Univariate ARIMA (AutoRegressive Integrated Moving Average) Modeling.
Long-memory time-series modeling.
Visual Data Mining
Visual Data Mining uses data and/or knowledge visualization techniques to discover implicit knowledge from large data sets. Visual data mining can be viewed as an integration of the following disciplines −
Data Visualization
Data Mining
Visual data mining is closely related to the following −
Computer Graphics
Multimedia Systems
Human Computer Interaction
Pattern Recognition
High-performance Computing
Generally data visualization and data mining can be integrated in the following ways −
-
Data Visualization − The data in a database or a data warehouse can be viewed in several visual forms that are listed below −
Boxplots
3-D Cubes
Data distribution charts
Curves
Surfaces
Link graphs etc.
Data Mining Result Visualization − Data Mining Result Visualization is the presentation of the results of data mining in visual forms. These visual forms could be scattered plots, boxplots, etc.
Data Mining Process Visualization − Data Mining Process Visualization presents the several processes of data mining. It allows the users to see how the data is extracted. It also allows the users to see from which database or data warehouse the data is cleaned, integrated, preprocessed, and mined.
Audio Data Mining
Audio data mining makes use of audio signals to indicate the patterns of data or the features of data mining results. By transforming patterns into sound and musing, we can listen to pitches and tunes, instead of watching pictures, in order to identify anything interesting.
Data Mining and Collaborative Filtering
Consumers today come across a variety of goods and services while shopping. During live customer transactions, a Recommender System helps the consumer by making product recommendations. The Collaborative Filtering Approach is generally used for recommending products to customers. These recommendations are based on the opinions of other customers.