C++ program to find the Area of the circumcircle of any triangles with sides given?

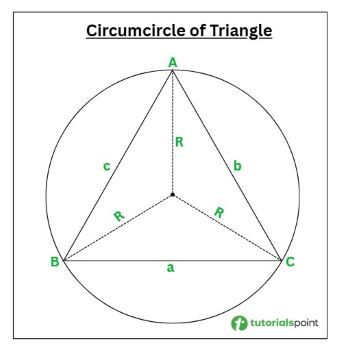
Circumcircle of Triangle

A circumcircle of a triangle is a circle that passes through all the vertices of a triangle. The center of circumcircle is known as the circumcenter, which is an intersection of all the perpendicular bisectors of the triangle. The radius is known as the circumradius and is denoted by R.

Formula to Calculate Area of Circumcircle of Triangle

You can use the formula given below to calculate the area of the circumcircle of a triangle:

$$ \frac{\pi (abc)^2}{16K^2} $$

where, a, b, and c are the sides of the triangle and k represents the area of the triangle and it is calculated using the Heron's formula:

$$K = \sqrt{s(s-a)(s-b)(s-c)} $$

where, s is the semi-perimeter of the triangle and can be calculated using the formula:

$$s = \frac{a+b+c}{2} $$

Here are some examples to find the area of the circumcircle of a triangle:

Scenario 1

Input: a = 4, b = 5, c = 3
Output: 19.625
Explanation:
Using the formula: Area = (pi * (a * b * c)^2) / (16 * K^2)
where K = sqrt(s * (s - a) * (s - b) * (s - c)) and s = (a + b + c) / 2
s = (4 + 5 + 3) / 2 = 6
K = sqrt(6 * (6 - 4) * (6 - 5) * (6 - 3)) 
= sqrt(6 * 2 * 1 * 3) = sqrt(36) = 6
Area = (3.14 * (4 * 5 * 3)^2) / (16 * 6^2)
Area = 11304 / 576 = 19.625

Scenario 2

Input: a = 7, b = 9, c = 13
Output: 146.722
Explanation:
Using the formula: Area = (pi * (a * b * c)^2) / (16 * K^2)
where K = sqrt(s * (s - a) * (s - b) * (s - c)) and s = (a + b + c) / 2
s = (7 + 9 + 13) / 2 = 14.5
K = sqrt(14.5 * (14.5 - 7) * (14.5 - 9) * (14.5 - 13)) 
= sqrt(14.5 * 7.5 * 5.5 * 1.5) = sqrt(897.1875)
Area = (3.14 * (7 * 9 * 13)^2) / (16 * 29.953^2)
Area = 2106189.54 / 14355 = 146.73

Formula Derivation

The circumradius can be represented as :

a/sinA = b/sinB = c/sinC = 2R
=> c/sin C = 2R
=> R = c/(2sinC)

The sinC can be represented as:

Area of the triangle (K)= 1/2 * base * height
K = 1/2 * a * (b * sinC)
=> sinC = 2 * K / (a * b)

Now the value of R becomes:

R = c/(2 * (2 * K / (a * b)))
R = (a * b * c) / (4 * K)

Using 'R' to calculate the area of circumcircle:

Area of circle = pi * R^2
Area of circumcircle = pi * ((a * b * c) / (4 * K))^2
Area of circumcircle = (pi * (a * b * c)^2) / (16 * K^2)

k = sqrt(s * (s - a) * (s - b) * (s - c)) [Heron's formula]
Area = (pi * (a * b * c)^2) / (16 * (s * (s - a) * (s - b) * (s - c)))

C++ Program to Find Area of Circumcircle of Triangle

In this example, we have used the above formula to calculate the area of the circumcircle of the triangle ABC:

#include <iostream>
#include <cmath>
using namespace std;

float area(float a, float b, float c)
{
   if (a < 0 || b < 0 || c < 0) // Sides should be positive
      return -1;
   float s = (a + b + c) / 2;
   float areaTriangle = sqrt(s * (s - a) * (s - b) * (s - c));
   float circumArea = 3.14 * pow(((a * b * c) / (4 * areaTriangle)), 2);
   return circumArea;
}
int main()
{
   float a = 4, b = 5, c = 3;
   cout << "Sides of the triangle are: " << a << ", " << b << ", " 
        << c << endl;
   cout << "Circumarea of the triangle: " << area(a, b, c);
}

The output of the above code is as follows:

Sides of the triangle are: 4, 5, 3
Circumarea of the triangle: 19.625