Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Counting Cache Misses in Data Structure
In algorithm analysis we count the operations and steps. This is basically justified when computer takes more time to perform an operation than they took to fetch the data needed for that operation. Nowadays the cost of performing an operation is significantly lower than the cost of fetching data from memory.
The run time of many algorithms is dominated by the number of memory references (number of cache misses) rather than by the number of operations. So, when we will try to desing some algorithms, we have to focus on reducing not only the number of operations but also the number of memory accesses. Also have to focus on designing algorithms that hide memory latency.
Suppose there is a simple computer model in which the computer’s memory consists of an L1 cache, an L2 cache, and main memory. We perform some Arithmetic and logical operations using ALU on data resident in registers (R)
This is the block diagram of it −
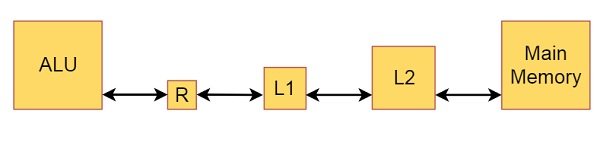
From the diagram we can also get some knowledge about the size of memory and caches. Main memory is basically hundreds or thousands of MB. Where L2 cache is some fraction of MBs and L1 caches are some KBs. The register size is some bits. When we execute a program, all data in memory. If we add some operation like ADD, then the first number will be stored into register, the data in registers are added, then result is written into memory.
Let one cycle be the length of time that will need to add data that are already in registers. The time is needed to load data from L1 cache to a register is suppose two cycles in this model. If the required data are not in L1 cache but present in L2 cache, we get an L1 cache miss and the required data are taken from L2 cache to L1 cache and the register in 10 cycles. When our required data are not in L2 cache also, we have an L2 cache miss and the required data will be taken from main memory into L2 cache, L1 cache, and the register in 100 cycles. Then the write operation is counted as one cycle even when the data are written to main memory, because we do not wait for the complete write before proceeding to the next operation
156 Views
