Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count ways to divide circle using N non-intersecting chords in C++
Given an integer N as input for a number of chords in a circle with 2*N end points. The goal is to count the ways in which we can divide that circle using such chords so that no chord intersects with each other.
For N=3, points will be 6, 1 way of getting 3 chords is between 1−2, 3−4, 5−6
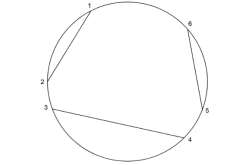
Other ways −
1−6, 2−5, 3−4 1−2, 3−6, 4−5 1−4, 2−3, 5−6 1−6, 2−3, 4−5
Total 5 ways.
For Example
Input
N=4
Output
Count of ways to divide circle using N non-intersecting chords are: 14
Explanation
There will be a total 8 points between which we can draw chords. After drawing the first chord, the rest of the points will be divided into two sets. No chord can be drawn between points from set 1 and set 2 as they will intersect with the first chord.
Input
N=6
Output
Count of ways to divide circle using N non−intersecting chords are: 132
Explanation
There will be a total 12 points between which we can draw chords. After drawing the first chord, the rest of the points will be divided into two sets. No chord can be drawn between points from set 1 and set 2 as they will intersect with the first chord.
Approach used in the below program is as follows −
In this approach we will count ways using previous counts. If we draw any chord between 2 points, the rest of the points will be divided into two sets set1 and set2, if we draw any chord between points in these two sets then they will intersect with the first chord.
Take an integer N as input.
Function divide_circle(int N) takes number and returns the count of ways to divide circle using N non−intersecting chords
Total number of points will be 2*N as total_points.
Take an array total_cuts[] storing the counts of ways.
For 0 or 2 points there will be only 1 way to initialize total_cuts[0], total_cuts[2] with 1.
For all other points starting from points=4, total ways will be ways with points i and rest n−i−1 points.
So take total_cuts[i] += (total_cuts[j] * total_cuts[i−2−j])
At the end we have total_cuts[ total_points ] as total number of ways.
Return total_cuts[ total_points ] as result at the end of the loop.
Example
#include <bits/stdc++.h>
using namespace std;
int divide_circle(int N){
int total_points = 2 * N;
int total_cuts[total_points + 1] = { 0 };
total_cuts[0] = 1;
total_cuts[2] = 1;
for (int i = 4; i <= total_points; i += 2){
for (int j = 0; j < i−1; j += 2){
total_cuts[i] += (total_cuts[j] * total_cuts[i−2−j]);
}
}
return total_cuts[total_points];
}
int main(){
int N = 3;
cout<<"Count of ways to divide circle using N non−intersecting chords are:"<<divide_circle(N);
return 0;
}Output
If we run the above code it will generate the following output −
Count of ways to divide circle using N non-intersecting chords are: 5
266 Views
To Continue Learning Please Login