Program to count how many ways we can divide the tree into two trees in Python

Suppose we have a binary tree containing values 0, 1 and 2. The root has at least one 0 node and one 1 node. Now suppose there is an operation where we delete an edge in the tree and the tree becomes two different trees. We have to find the number of ways we can delete one edge such that none of the two trees contain both a 0 node and a 1 node.

So, if the input is like

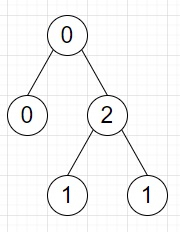
then the output will be 1 as we can only delete the 0 to 2 edge.

To solve this, we will follow these steps −

• count := [0, 0, 0]
• Define a function dfs() . This will take node
• if node is not null, then
  • pre := count
  • dfs(left of node)
  • dfs(right of node)
  • count[value of node] := count[value of node] + 1
  • node.count := a list of (count[i] - pre[i]) for i is 0 and 1
• Define a function dfs2() . This will take node, par
• if node is not null, then
  • if par is not null, then
    • (a0, a1) := count of node
    • (b0, b1) := (count[0] - a0, count[1] - a1)
    • if (a0 is same as 0 or a1 is same as 0) and (b0 is same as 0 or b1 is same as 0), then
      • ans := ans + 1
  • dfs2(left of node, node)
  • dfs2(right of node, node)
• From the main method, do the following −
• dfs(root)
• ans := 0
• dfs2(root)
• return ans

Let us see the following implementation to get better understanding −

Example

 Live Demo

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.val = data
      self.left = left
      self.right = right
class Solution:
   def solve(self, root):
      count = [0, 0, 0]
   def dfs(node):
      if node:
         pre = count[:]
         dfs(node.left)
         dfs(node.right)
         count[node.val] += 1
         node.count = [count[i] - pre[i] for i in range(2)]
   dfs(root)
   def dfs2(node, par=None):
      if node:
         if par is not None:
            a0, a1 = node.count
            b0, b1 = count[0] - a0, count[1] - a1
            if (a0 == 0 or a1 == 0) and (b0 == 0 or b1 == 0):
               self.ans += 1
         dfs2(node.left, node)
         dfs2(node.right, node)
   self.ans = 0
   dfs2(root)
   return self.ans
ob = Solution()
root = TreeNode(0)
root.left = TreeNode(0)
root.right = TreeNode(2)
root.right.left = TreeNode(1)
root.right.right = TreeNode(1)
print(ob.solve(root))

Input

root = TreeNode(0)
root.left = TreeNode(0)
root.right = TreeNode(2)
root.right.left = TreeNode(1)
root.right.right = TreeNode(1)

Output

1

Arnab Chakraborty

Published on 20-Oct-2020 07:29:38

• Related Questions & Answers
• Program to count how many ways we can cut the matrix into k pieces in python
• C++ program to count in how many ways we can paint blocks with two conditions
• Program to find how many ways we can climb stairs in Python
• C++ program to count in how many ways we can minimize cable length to connect computers
• In how many ways we can concatenate Strings in Java?
• Program to check how many ways we can choose empty cells of a matrix in python
• How many ways can we read data from the keyboard in Java?
• Program to count number of ways we can throw n dices in Python
• In how many ways can we split a string in JavaScript?
• Program to count number of ways we can distribute coins to workers in Python
• Program to find how many ways we can climb stairs (maximum steps at most k times) in Python
• C++ program to count how many ways two players win or make draw in dice throwing game
• How can we divide the result set returned by MySQL into groups?
• Program to find out how many boxes can be put into the godown in Python
• What are JSP declarations? In how many ways we can write JSP declarations?