Count number of squares in a rectangle in C++

We are given with a rectangle of length L and breadth B, such that L>=B. The goal is to find the number of squares that a rectangle of size LXB can accommodate.

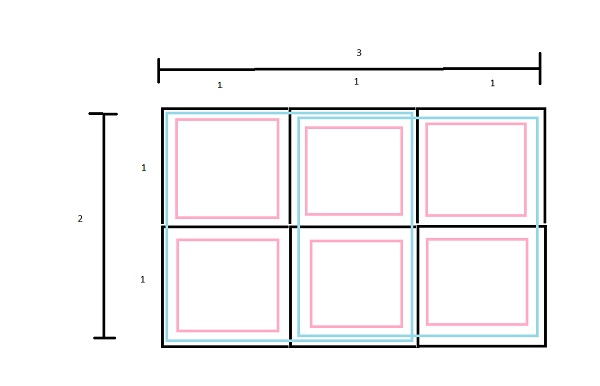
Above figure shows a rectangle of size 3 X 2. It has 2, 2X2 squares and 6,1X1 squares in it.

Total squares= 6+2=8.

Every rectangle of size LXB has L*B number of 1X1 squares.
Biggest squares are of size BXB.
For L=B=1, squares = 1.
For L=B=2, squares = 1 + 4 = 5. ( 1 of 2X2, 4 of 1X1 )
For L=B=3, squares = 1 + 4 + 9 = 14. ( 1 of 3X3, 4 of 2X2, 9 of 1X1 )
For L=B=4, squares = 1 + 4 + 9 + 16 = 30 ( 1 of 4X4, 4 of 3X3, 9 of 2X2, 16 of 1X1 )
……………..
For every BXB rectangle number of squares is

for ( i=1 to B )
No. of squares + = i*i.

When L>B. More squares will be added. When L=B+1 ( 1 extra column than B ). Then squares added will be L + ( L-1) + ….+3+2+1 = L(L+1)/2

So for extra L-B columns squares added will be ( L-B ) * (B)(B+1)/2

Total squares will be squares in BXB + (L-B) * (L)(L+1)/2.
You can also use formula B(B+1)(2B+1)/6 for the series (1 + 4 + 9 +......BXB) in step 8.

Let’s understand with examples.

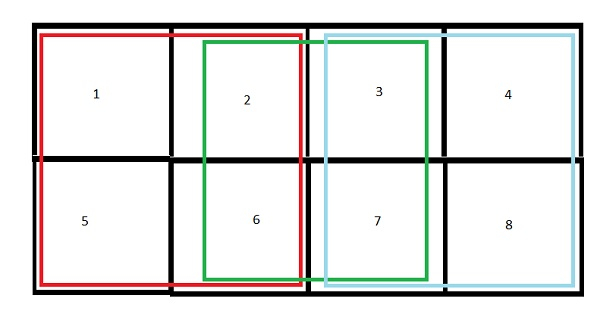
Input − L=4, B=2

Output − Count of squares in rectangle − 11

Explanation − 8 squares of 1X1 and 3 of 2X2.

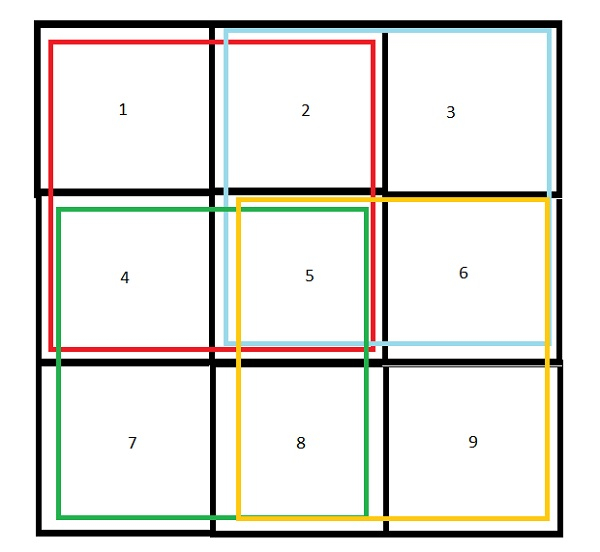
Input − L=3, B=3

Output − Count of squares in rectangle − 14

Explanation − 9 squares of 1X1 , 4 of 2X2 and 1 of 3X3.

Approach used in the below program is as follows

We take an integers length and breadth for dimensions of rectangle.
Function numofSquares(int l, int b) takes dimensions and returns the number of squares in the rectangle of size lXb.
For biggest squares bXb. Use for loop from 1 to b and add each i*i to squares.
Now if l>b. New added squares will be (l-b)(b)(b+1)/2. Add this to squares.
Return squares as desired result.

Note − keeping length>=breadth

Example

Live Demo

#include<iostream>
using namespace std;
int numofSquares(int l, int b){
   int squares=0;
   for(int i=1;i<=b;i++) //squares inside biggest square of size breadth X breadth{
      squares += i*i;
   }
   squares+=(l-b)*b*(b+1)/2;
   return squares;
}
int main(){
   int length = 5, breadth = 4; //keep length always >= breadth
   cout << "Count of squares is :"<< numofSquares(length,breadth);
}