Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Conway’s Game Of Life using Python?
A British mathematician in an around 1970 created his “Game of Life” – which are basically a set of rules depicting the chaotic yet patterned growth of a colony of biological organisms. The “Game of Life” is a two-dimensional grid consists of “living” and “dead” cells.
Rules of Game of life
Overpopulation: A cell dies(off) if its surrounded by more than three living cells.
Static: A cell lives(on) if its surrounded by two or three living cells.
Underpopulation: A cell dies(off) if its surrounded by fewer than two living cells.
Reproduction: A cell becomes live(on) if a dead cell is surrounded by exactly three cells.
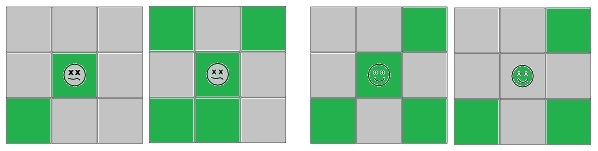
Cell is going to die in the next timestamp
Cell is going to live in the next timestamp
Cell is alive
Cell is dead
By applying above set of rules in sequential steps we’ll get beautiful and unexpected patterns.
Steps of implementation:
i. Initialise an empty universe ii. Fill the universe with the seed iii. Calculate if the current cell survives to the next timestamps, based on its neighbours iv. Repeat this survival function(like step-iii) over all the cells in the universe neighbours. v. Repeat steps iii-iv for the desired number of generations.
Installation:
To create conways game of life we are going to use, matplotlib and numpy arrays library. To install numpy and matplolib, use pip-
$pip install numpy, matplolib
Program to implement conways game of life:
Now it’s time to write program as per our above set of rules. Below is the program to implement game of life,
#Import required library
import numpy as np
import matplotlib.pyplot as plt
import argparse
import time
#-------------------------------------------------------------------------
class Board(object):
def __init__(self, size, seed = 'Random'):
if seed == 'Random':
self.state = np.random.randint(2, size = size)
self.engine = Engine(self)
self.iteration = 0
def animate(self):
i = self.iteration
im = None
plt.title("Conway's Game of Life")
while True:
if i == 0:
plt.ion()
im = plt.imshow(self.state, vmin = 0, vmax = 2, cmap = plt.cm.gray)
else:
im.set_data(self.state)
i += 1
self.engine.applyRules()
print('Life Cycle: {} Birth: {} Survive: {}'.format(i, self.engine.nBirth, self.engine.nSurvive))
plt.pause(0.01)
yield self
#-------------------------------------------------------------------------
class Engine(object):
def __init__(self, board):
self.state = board.state
def countNeighbors(self):
state = self.state
n = (state[0:-2,0:-2] + state[0:-2,1:-1] + state[0:-2,2:] +
state[1:-1,0:-2] + state[1:-1,2:] + state[2:,0:-2] +
state[2:,1:-1] + state[2:,2:])
return n
def applyRules(self):
n = self.countNeighbors()
state = self.state
birth = (n == 3) & (state[1:-1,1:-1] == 0)
survive = ((n == 2) | (n == 3)) & (state[1:-1,1:-1] == 1)
state[...] = 0
state[1:-1,1:-1][birth | survive] = 1
nBirth = np.sum(birth)
self.nBirth = nBirth
nSurvive = np.sum(survive)
self.nSurvive = nSurvive
return state
#-------------------------------------------------------------------------
def main():
ap = argparse.ArgumentParser(add_help = False) # Intilialize Argument Parser
ap.add_argument('-h', '--height', help = 'Board Height', default = 256)
ap.add_argument('-w', '--width', help = 'Board Width', default = 256)
args = vars(ap.parse_args()) # Gather Arguments
bHeight = int(args['height'])
bWidth = int(args['width'])
board = Board((bHeight,bWidth))
for _ in board.animate():
pass
#-------------------------------------------------------------------------
if __name__ == '__main__':
main()Output
Console: Life Cycle: 1 Birth: 7166 Survive: 10621 Life Cycle: 2 Birth: 7930 Survive: 8409 Life Cycle: 3 Birth: 7574 Survive: 8756 Life Cycle: 4 Birth: 7114 Survive: 8406 Life Cycle: 5 Birth: 7005 Survive: 8126 Life Cycle: 6 Birth: 6644 Survive: 7926 Life Cycle: 7 Birth: 6266 Survive: 7711 Life Cycle: 8 Birth: 6132 Survive: 7427 Life Cycle: 9 Birth: 5957 Survive: 7322 Life Cycle: 10 Birth: 5769 Survive: 7290 Life Cycle: 11 Birth: 5585 Survive: 6937 Life Cycle: 12 Birth: 5381 Survive: 6791 Life Cycle: 13 Birth: 5208 Survive: 6686 Life Cycle: 14 Birth: 5063 Survive: 6563 …. …
Above results will be keep coming till we hit Ctrl-C in our terminal to stop program.
Graphical display:
Cells will keeps altering and will simulate very beautiful pattern.
You can change the above subplot by changing the settings and alter the slider value:
441 Views
