- Convex Optimization Tutorial
- Home
- Introduction
- Linear Programming
- Norm
- Inner Product
- Minima and Maxima
- Convex Set
- Affine Set
- Convex Hull
- Caratheodory Theorem
- Weierstrass Theorem
- Closest Point Theorem
- Fundamental Separation Theorem
- Convex Cones
- Polar Cone
- Conic Combination
- Polyhedral Set
- Extreme point of a convex set
- Direction
- Convex & Concave Function
- Jensen's Inequality
- Differentiable Convex Function
- Sufficient & Necessary Conditions for Global Optima
- Quasiconvex & Quasiconcave functions
- Differentiable Quasiconvex Function
- Strictly Quasiconvex Function
- Strongly Quasiconvex Function
- Pseudoconvex Function
- Convex Programming Problem
- Fritz-John Conditions
- Karush-Kuhn-Tucker Optimality Necessary Conditions
- Algorithms for Convex Problems
- Convex Optimization Resources
- Convex Optimization - Quick Guide
- Convex Optimization - Resources
- Convex Optimization - Discussion
Convex Optimization - Minima and Maxima
Local Minima or Minimize
$\bar{x}\in \:S$ is said to be local minima of a function $f$ if $f\left ( \bar{x} \right )\leq f\left ( x \right ),\forall x \in N_\varepsilon \left ( \bar{x} \right )$ where $N_\varepsilon \left ( \bar{x} \right )$ means neighbourhood of $\bar{x}$, i.e., $N_\varepsilon \left ( \bar{x} \right )$ means $\left \| x-\bar{x} \right \|< \varepsilon$
Local Maxima or Maximizer
$\bar{x}\in \:S$ is said to be local maxima of a function $f$ if $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \bar{x} \right )$ where $N_\varepsilon \left ( \bar{x} \right )$ means neighbourhood of $\bar{x}$, i.e., $N_\varepsilon \left ( \bar{x} \right )$ means $\left \| x-\bar{x} \right \|< \varepsilon$
Global minima
$\bar{x}\in \:S$ is said to be global minima of a function $f$ if $f\left ( \bar{x} \right )\leq f\left ( x \right ), \forall x \in S$
Global maxima
$\bar{x}\in \:S$ is said to be global maxima of a function $f$ if $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in S$
Examples
Step 1 − find the local minima and maxima of $f\left ( \bar{x} \right )=\left | x^2-4 \right |$
Solution −
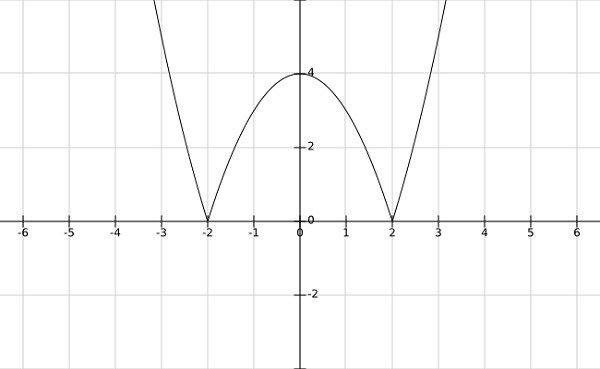
From the graph of the above function, it is clear that the local minima occurs at $x= \pm 2$ and local maxima at $x = 0$
Step 2 − find the global minima af the function $f\left (x \right )=\left | 4x^3-3x^2+7 \right |$
Solution −
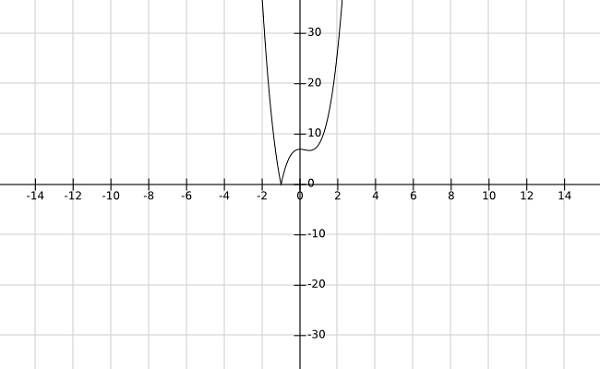
From the graph of the above function, it is clear that the global minima occurs at $x=-1$.