Check if matrix A can be converted to B by changing parity of corner elements of any submatrix in Python

Suppose we have two N X M binary matrices A and B. In a single operation, we can select a sub-matrix (at least 2x2) and convert the parity of the corner elements (flip bits). Finally, we have to check whether the matrix A can be converted to B by performing any number of operations or not.

So, if the input is like

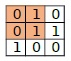
then the output will be True as we can perform the operation on the top left square sub-matrix of size (2x2) on mat1 to get mat2.

To solve this, we will follow these steps −

• row := row count of mat1
• column := column count of mat1
• for i in range 1 to row - 1, do
  • for j in range 1 to column - 1, do
    • if mat1[i, j] is not same as mat2[i, j], then
      • mat1[i, j] := mat1[i, j] XOR 1
      • mat1[0, 0] := mat1[0, 0] XOR 1
      • mat1[0, j] := mat1[0, j] XOR 1
      • mat1[i, 0] := mat1[i, 0] XOR 1
• for i in range 0 to row - 1, do
  • for j in range 0 to column - 1, do
    • if mat1[i, j] is not same as mat2[i, j], then
      • return False
• return True

Example

Let us see the following implementation to get better understanding −

 Live Demo

def solve(mat1, mat2):
   row = len(mat1)
   column = len(mat1[0])
   for i in range(1, row):
      for j in range(1, column):
         if mat1[i][j] != mat2[i][j]:
            mat1[i][j] ^= 1
            mat1[0][0] ^= 1
            mat1[0][j] ^= 1
            mat1[i][0] ^= 1
   for i in range(row):
      for j in range(column):
         if mat1[i][j] != mat2[i][j]:
            return False
   return True
mat1 = [
         [1, 0, 0],
         [1, 0, 1],
         [1, 0, 0]]
mat2 = [
         [0, 1, 0],
         [0, 1, 1],
         [1, 0, 0]]
print(solve(mat1, mat2))

Input

[
   [1, 0, 0],
   [1, 0, 1],
   [1, 0, 0]],
[
   [0, 1, 0],
   [0, 1, 1],
   [1, 0, 0]]

Output

True

Arnab Chakraborty

Updated on 19-Jan-2021 04:52:26

• Related Questions & Answers
• Check if matrix can be converted to another matrix by transposing square sub-matrices in Python
• How to check if a string can be converted to float in Python?
• Check if a string can be converted to another string by replacing vowels and consonants in Python
• Check if a number can be expressed as a^b in Python
• Check if given string can be formed by concatenating string elements of list in Python
• Check if elements of array can be made equal by multiplying given prime numbers in Python
• How I can check if A is superclass of B in Python?
• Check if N can be represented as sum of integers chosen from set {A, B} in Python
• Check if a number can be expressed as a^b in C++
• Program to check one string can be converted to other by shifting characters clockwise in Python
• Program to check one string can be converted to another by removing one element in Python
• Parity Check of a Number
• Check If every group of a is followed by a group of b of same length in Python
• Check if any permutation of a large number is divisible by 8 in Python
• Check if elements of an array can be arranged satisfying the given condition in Python