Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Search in C++ program?
binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array. Even though the idea is simple, implementing binary search correctly requires attention to some subtleties about its exit conditions and midpoint calculation, particularly if the values in the array are not all of the whole numbers in the range.
Binary search is the most popular search algorithm. It is efficient and also one of the most commonly used techniques that are used to solve problems.
If all the names in the world are written down together in order and you want to search for the position of a specific name, binary search will accomplish this in a maximum of 35 iterations.
Binary search works only on a sorted set of elements. To use binary search on a collection, the collection must first be sorted.
When a binary search is used to perform operations on a sorted set, the number of iterations can always be reduced on the basis of the value that is being searched.
Let us consider the following array −
By using a linear search, the position of element 8 will be determined in the 9th iteration.
Let's see how the number of iterations can be reduced by using a binary search. Before we start the search, we need to know the start and end of the range. Let's call them Low and High.
Low = 0 High = n-1
Now, compare the search value K with the element located at the median of the lower and upper bounds. If the value K is greater, increase the lower bound, else decrease the upper bound.
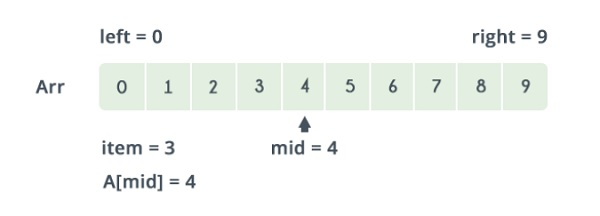
Referring to the image above, the lower bound is 0 and the upper bound is 9
The median of the lower and upper bounds is (lower_bound + upper_bound) / 2 = 4. Here a[4] = 4. The value 4>2, which is the value that you are searching for. Therefore, we do not need to conduct a search on any element beyond 4 as the elements beyond it will obviously be greater than 2.
Therefore, we can always drop the upper bound of the array to the position of element 4. Now, we follow the same procedure on the same array with the following values −
Low: 0 High: 3
Repeat this procedure recursively until Low > High. If at any iteration, we get a[mid]=key, we return value of mid. This is the position of key in the array. If key is not present in the array, we return −1.
Example
int binarySearch(int low,int high,int key){
while(low<=high){
int mid=(low+high)/2;
if(a[mid]<key){
low=mid+1;
}
else if(a[mid]>key){
high=mid-1;
}
else{
return mid;
}
}
return -1; //key not found
}
644 Views
To Continue Learning Please Login