Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Barnsley Fern in Python
In this tutorial, we are going to learn about the Barnsley Fern, which is created by Michael Barnsley. The features of Barnsley Fern is similar to the fern shape. It is created by iterating over the four mathematical equations known as Iterated Function System(IFS). The transformation has the following formula.
f(x,y)=$$\begin{bmatrix}a & b \c & d \end{bmatrix}\begin{bmatrix}x \y \end{bmatrix}+\begin{bmatrix}e \f \end{bmatrix}$$
Source − Wikipedia
The values of the variables are −
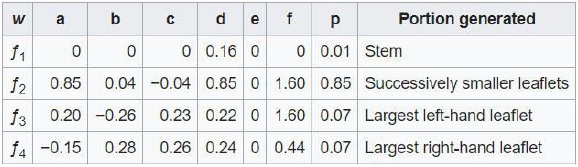
Source − Wikipedia
The four equation that Barnsley Fern proposed are −
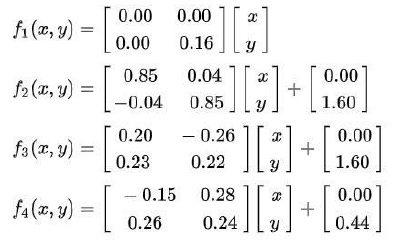
Source − Wikipedia
Now, we will see code to create the fern shape in Python.
Example
# importing matplotlib module for the plot import matplotlib.pyplot as plot # importing random module to generate random integers for the plot import random # initialising the lists x = [0] y = [0] # initialising a variable to zero to track position current = 0 for i in range(1, 1000): # generating a random integer between 1 and 100 z = random.randint(1, 100) # checking the z range and appending corresponding values to x and y # appending values to the x and y if z == 1: x.append(0) y.append(0.16 * y[current]) if z >= 2 and z <= 86: x.append(0.85 * x[current] + 0.04 * y[current]) y.append(-0.04 * x[current] + 0.85 * y[current] +1.6) if z>= 87 and z<= 93: x.append(0.2 * x[current] - 0.26 * y[current]) y.append(0.23 * x[current] + 0.22*(y[current])+1.6) if z >= 94 and z <= 100: x.append(-0.15 * x[current] + 0.28 * y[current]) y.append(0.26 * x[current] + 0.24 * y[current] + 0.44) # incrementing the current value current += 1 # plotting the graph using x and y plot.scatter(x, y, s = 0.2, edgecolor = 'green') plot.show()
Output
If you run the above code, you will get the following result.
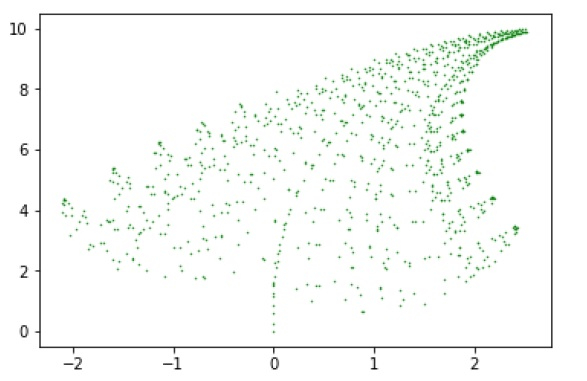
Conclusion
If you have any doubts in the tutorial, mention them in the comment section. Reference −Wikipedia
272 Views
