
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Arranging Coins in C++
In this problem, we have n number of coins. To arrange these coins in a staircase shape such that each row consists of k number of coins, where k is the row number in which the coins are placed. The last row may or may not be completely filled. Our task is to find the number of completely filled rows.
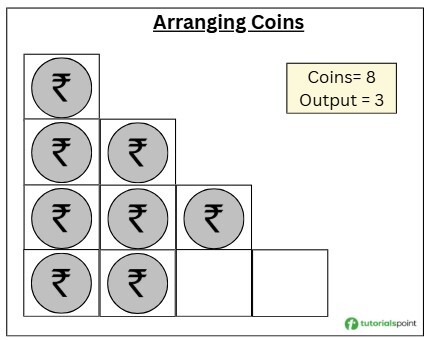
Here is a scenario of arranging coins problem:
Scenario
Input: n = 8 Output: 3 Explanation: In the above figure, we can see there are 3 completely filled rows and the last row has 2 filled columns and 2 empty columns. => Output = 3
Formula for Arranging Coins
The formula to find the number of completely filled rows is given below:
$$ \frac{\sqrt{8n+1} - 1}{2} $$The derivation of the above formula is given below:
Suppose the number of rows is k and the number of coins is n. Number of coins in first row = 1 Number of coins in the second row = 2 . . Number of coins in kth row = k => Sum of natural numbers upto k = (k(k+1))/2 => n = (k(k+1))/2 (when rows are completely filled) => k(k+1)/2 < n (when the last row is partially filled) => k(k+1) <= 2n (Combining above two equations) => k^2 + k - 2n <= 0 => k = (-1 + sqrt(1 + 8n))/2 (ignored the negative root)
Example
Here is an example to find out the number of completely filled rows with coins:
Input: n = 8 Output: 3 Explanation: Using the above formula: k = (-1 + sqrt(1 + 8*n))/2 = (-1 + sqrt(1 + 8*8))/2 = (-1 + sqrt(65))/2 = (-1 + 8.06)/2 = 3.53 (approx) Since coins can not be in decimal Therefore, k = 3
Implementing Arranging Coins Problem in C++
To get the number of completely filled rows, we will use the above formula in the code. For calculating the square root, we have used the sqrt() function.
The following example finds the number of completely filled rows when the number of coins is given as 13:
#include <bits/stdc++.h>
using namespace std;
int arrangeCoins(int n)
{
return (sqrt(8 * (long long)n + 1) - 1) / 2;
}
int main()
{
int n = 13;
cout << "Number of coins: " << n << endl;
cout << "Number of completely filled staircase rows: ";
cout << arrangeCoins(n) << endl;
return 0;
}
The output of the above code is as follows:
Number of coins: 13 Number of completely filled staircase rows: 4
Conclusion
In this article, we have discussed arranging coins problem where we find the number of completely filled rows of coins. We discussed the formula and its derivation to solve this problem with an example C++ code.

