Area of Pentagon

Introduction

Area of pentagon is the region enclosed by the boundaries of pentagon. A polygon with five straight sides is called a pentagon. The majority of math class tasks will include normal pentagons, which have five equal sides. Depending on the amount of information you have, there are two typical methods for finding the location. The region that is surrounded by a pentagon's five sides is known as the area of the pentagon. A pentagon is a five-sided polygon that has only two dimensions. The Greek words "Penta" (which means "five") and "gon" (which means "angles") are the source of its name. Using examples that have been solved and practice questions, we will learn how to determine the area of the pentagon in this tutorial.

Pentagons

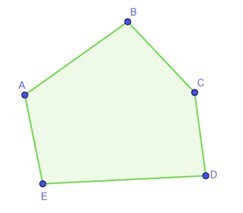
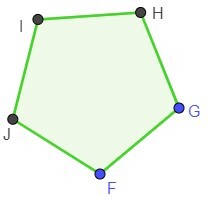
In geometry, a pentagon is any five-sided polygon or 5-gon (from the Greek word pente meaning five and gonia meaning angle. In a straightforward pentagon, the interior angles add up to 540°. A pentagon could be straightforward or self-intersect. A pentagram is a self-intersecting regular pentagon (sometimes known as a star pentagon). In the following figure, ABCDE is an irregular pentagon and FGHIJ is a regular pentagon

Area of a Pentagon

• The space enclosed by a pentagon's sides is referred to as the pentagon's area. Various techniques can be used to compute it depending on the dimensions that are known.

• The kind of pentagon also makes a difference. For instance, if it is a normal pentagon, the area can be determined using a single formula; but, if it is an irregular pentagon, we must divide it into various polygons and add their areas to determine the pentagon's area.

• Depending on the type of pentagon, a different formula is employed to calculate its area.

• The formula for finding the area of a regular pentagon that is frequently employed is,

  $$\mathrm{Area\: of\: the\: pentagon\: equals\: \frac{1}{2}×pa}$$

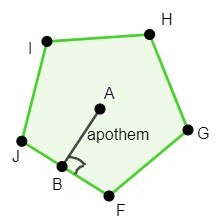
  Here, "p" stands for the pentagon's perimeter, while "a" stands for its apothem. See the apothem "a" and the side-length "s" in the following pentagon.

Example:

Find the area of a regular pentagon with 15 units of side length and 4 units of apothem.

Answer:

Given that s=15 & apothem=4

Using the apothem formula stated above we will determine the area of the regular pentagon s follows −

$$\mathrm{Area\: of\: the\: pentagon\: = \frac{1}{2}×pa}$$

Here let us calculate the value of perimeter by p=5s=5(15)=75 sq. units.

Thus,

$$\mathrm{Area\: of\: the\: pentagon\: = \frac{1}{2}×75×4=75×2=150 units}$$

• If you just know the side length "s," you can determine the area of a regular pentagon. The equation for calculating the surface area of a regular pentagon, $\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$ where s is the length of the one of the side of the regular pentagon

Example:

Determine the area of a pentagon with a side length of 5 units.

Answer:

Given that,

s=5 units

Thus, employing the area of pentagon formula, we get

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$$

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 5^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 25}=\frac{25}{4}\sqrt{5(5+2\sqrt{5})}\:sq. units}$$

• The area of an irregular pentagon can be computed by dividing it into smaller polygons. The area of each polygon is then calculated and added together to yield the area of the pentagon.

Solved Examples

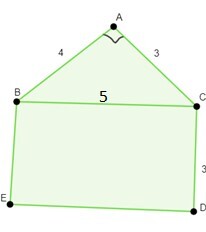
1)Determine the area of the following Pentagon which is an irregular pentagon

Answer:

Notice that in pentagon ABCDE, triangle ABC is a right triangle and quadrilateral BEDC is a rectangle.

Thus, the required area of the pentagon is the sum of the areas of these two regions, that is the sum of the area of triangle ABC and the rectangle BEDC.

Notice that $\mathrm{a(ΔABC)=\frac{1}{2}×base ×height=\frac{1}{2}×3×4=6\: sq. units}$

$$\mathrm{a(BEDC)=3×BC=3×5=15\: sq. units}$$

Thus, the area of pentagon ABCDE is given by

$$\mathrm{a(ABCDE)=6+15=21\: sq. units}$$

2)Determine the area of a pentagon with a side length of 8 units.

Answer:

Given that,

s=8 units

Thus, employing the area of pentagon formula, we get

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$$

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 8^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 64}=\frac{64}{4}\sqrt{5(5+2\sqrt{5})}\:sq. units}$$

3)Find the area of a regular pentagon with 20 units of side length and 6 units of apothem.

Answer:

Given that s=20 & apothem=6

Using the apothem formula stated above we will determine the area of the regular pentagon as follows:

Area of the pentagon =$\mathrm{\frac{1}{2}×pa}$

Here let us calculate the value of perimeter by p=5s=5(20)=100 units.

Thus,

Area of the pentagon =$\mathrm{\frac{1}{2}\times 100 \times 6=100\times 3=300\: sq. units}$

4)Find the area of a regular pentagon with 13 units of side length and 6 units of apothem.

Answer:

Given that s=13 & apothem=6

Using the apothem formula stated above we will determine the area of the regular pentagon as follows −

Area of the pentagon =$\mathrm{\frac{1}{2}×pa}$

Here let us calculate the value of perimeter by p=5s=5(13)=65 units.

Thus,

Area of the pentagon =$\mathrm{\frac{1}{2}\times 65 \times 6=65 \times 3=195\: sq. units}$

5)Calculate the area of a pentagon with a side length of 11 units.

Answer :

Given that,

s=11 units

Thus, employing the area of pentagon formula, we get

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$$

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 11^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 121}=\frac{121}{4}\sqrt{5(5+2\sqrt{5})}\:sq. units}$$

6)Calculate the area of a pentagon with a side length of 17 units.

Answer:

Given that,

s=17 units

Thus, employing the area of pentagon formula, we get

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$$

$$\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 17^{2}}=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) 289}=\frac{289}{4}\sqrt{5(5+2\sqrt{5})}\:sq. units}$$

Conclusion

• A pentagon is a 5 sided and 5 angles based polygon

• It can be regular or irregular

• The sum of the interior angles in a pentagon is 540 degrees

• Area of the pentagon =$\mathrm{\frac{1}{2}×pa}$ when the apothem of pentagon is known.

• $\mathrm{A=\frac{1}{4}\sqrt{5(5+2\sqrt{5}) s^{2}}}$ when side of regular pentagon is given

FAQs

1. Are all the angles in a pentagon the same?

A regular pentagon has five equal sides and five equal angles. As a result, the formula below calculates the internal angles of a regular pentagon.

2. How many different kinds of pentagons are there?

A pentagon is a five-sided geometric shape with five angles. "Penta" stands for five, and "gon" stands for angle. One of the types of polygons is the pentagon. A regular pentagon's interior angles add up to 540 degrees.

3. Is it true that a pentagon is always a polygon?

A pentagon has five sides and five angles. A polygon is what it is. Polygons are shapes with closed, straight sides and angles. Regular and irregular polygons, including pentagons, exist.

4. What is the number of angles in a pentagon?

A pentagon has five interior angles.

5. Is it possible for a pentagon to be concave?

Pentagons and other polygons can also be either convex or concave. A pentagon or polygon is convex if all of its interior angles are less than 180°. It is concave if one or more interior angles are greater than 180°. A convex pentagon is always a regular pentagon.

6. Is it possible for a pentagon to be convex?

Pentagons and other polygons can also be either convex or concave. A pentagon or polygon is convex if all of its interior angles are less than 180°. It is concave if one or more interior angles are greater than 180°. A convex pentagon is always a regular pentagon.

7. What is a pentagon's apothem?

Apothem is the line that runs from the centre of the pentagon to a side and intersects the side at a right angle of 90 degrees.