
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Amortized time complexity in Data Structures
Amortize Analysis
This analysis is used when the occasional operation is very slow, but most of the operations which are executing very frequently are faster. In Data structures we need amortized analysis for Hash Tables, Disjoint Sets etc.
In the Hash-table, the most of the time the searching time complexity is O(1), but sometimes it executes O(n) operations. When we want to search or insert an element in a hash table for most of the cases it is constant time taking the task, but when a collision occurs, it needs O(n) times operations for collision resolution.
Aggregate Method
The aggregate method is used to find the total cost. If we want to add a bunch of data, then we need to find the amortized cost by this formula.
For a sequence of n operations, the cost is −
$\frac{Cost ( n\:operations)}{n}=\frac{Cost (normal\:operations)+Cost (Expensive\:operations)}{n}$
Example on Amortized Analysis
For a dynamic array, items can be inserted at a given index in O(1) time. But if that index is not present in the array, it fails to perform the task in constant time. For that case, it initially doubles the size of the array then inserts the element if the index is present.
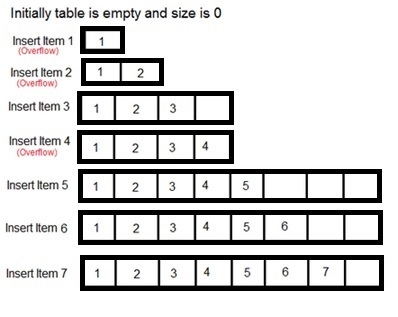
For the dynamic array, let ci = cost of ith insertion.
$So\:ci=1+\begin{cases}i\:-\:1,if\:i-1\:is\:power\:of\:2 \0, \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:Otherwise\end{cases}$
$$\frac{\displaystyle\sum\limits_{i=1}^n ci}{n}\leq\frac{n+\displaystyle\sum\limits_{j=1}^{\lfloor\log{2}{\lgroup n-1\rgroup}\rfloor} 2j}{n}=\frac{O\lgroup n\rgroup}{n}$$

