
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Add One Row to Tree in C++
We are given the root of a binary tree and two integers, val and depth. The root of the binary tree is at depth 1. Our task is to add a new row of nodes with value val at the given depth.
If the depth is 1, we have to create a new root node with value val and make the original tree its left child. If the depth is greater than 1, we go to all nodes at depth depth - 1, add new left and right child nodes with value val, and connect the original left and right subtrees under them.
Let's look at the example scenarios below to understand it better-
Scenario 1
Input: root = [7,3,9,1,5], val = 10, depth = 3 Output: (level-order traversal) [7,3,9,10,10,10,10,1,5]Explanation: We are adding a new row of nodes with value 10 at depth 3.
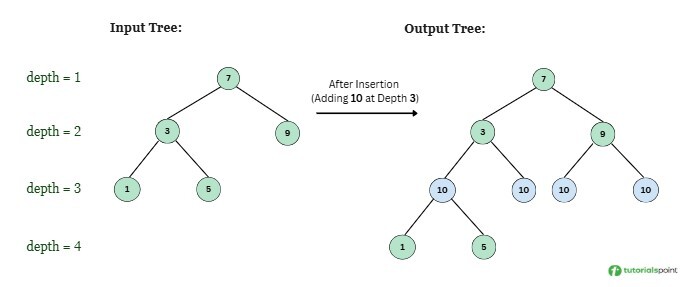
Scenario 2
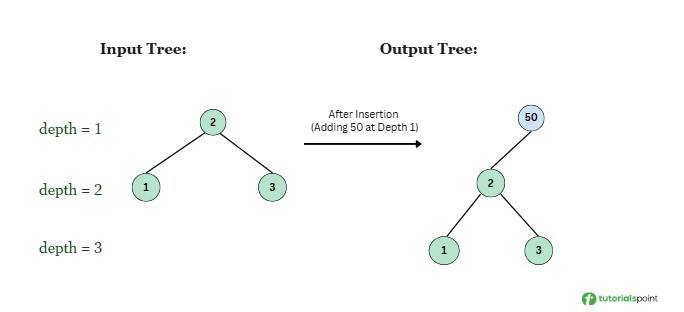
Input:root = [2,1,3], val = 50, depth = 1 Output: (level-order traversal) [50, 2, null, 1, 3]
Explanation: Since the depth is 1, we insert a new root with the value 50 and make the original tree its left child.
We can add a new row to a binary tree using two main methods:
Let's look at both one by one.
Breadth First Search (BFS)
To add a new row at the given depth, we use breadth-first search (also called level-order traversal). It helps us move through the tree one level at a time using a queue, until we reach depth-1. Once we reach that level, we perform the insertion.
Algorithm
The following are the steps:
- We first check if the given depth is 1. If yes, we create a new root node with the given value and attach the original tree as its left child. This handles the base case.
- If not, we start level order traversal using a queue. We push the root node into the queue and set the current depth to 1.
- We move level by level. At each level, we process all nodes in the queue and push their left and right children into the queue. We continue this until we reach depth-1.
- At this level, for each node, we store its original left and right children and create two new nodes with the given value.
- We then set the new left node as the left child and attach the original left subtree under it. Similarly, we set the new right node as the right child and attach the original right subtree under it.
Example
The following C++ program adds a new row to a binary tree at the given depth using level order traversal (BFS).
#include<iostream>
#include<queue>
using namespace std;
// TreeNode definition
struct TreeNode {
int val;
TreeNode * left;
TreeNode * right;
TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
};
// Function to insert a row at given depth
TreeNode * insertRow(TreeNode * root, int val, int depth) {
if (depth == 1) {
TreeNode * newRoot = new TreeNode(val);
newRoot ->
left = root;
return newRoot;
}
queue <
TreeNode * >
q;
q.push(root);
int currDepth = 1;
// Level order traversal to reach the depth-1 level
while (!q.empty()) {
int levelSize = q.size();
if (currDepth == depth-1) {
// We are at the level just before the target depth
while (levelSize--) {
TreeNode * node = q.front();
q.pop();
TreeNode * oldLeft = node ->
left;
TreeNode * oldRight = node ->
right;
// Insert new nodes and reattach the old children
node ->
left = new TreeNode(val);
node ->
left ->
left = oldLeft;
node ->
right = new TreeNode(val);
node ->
right ->
right = oldRight;
}
break;
} else {
// Traverse to the next level
while (levelSize--) {
TreeNode * node = q.front();
q.pop();
if (node -> left) q.push(node -> left);
if (node -> right) q.push(node -> right);
}
currDepth++;
}
}
return root;
}
// Function to print the tree level by level
void printTreeByLevels(TreeNode * root) {
if (!root) return;
queue <
TreeNode * >
q;
q.push(root);
while (!q.empty()) {
int size = q.size();
while (size--) {
TreeNode * node = q.front();
q.pop();
cout <<
node ->
val <<
" ";
if (node -> left) q.push(node -> left);
if (node -> right) q.push(node -> right);
}
cout <<
"\n";
}
}
int main() {
TreeNode * root = new TreeNode(4);
root ->
left = new TreeNode(2);
root ->
right = new TreeNode(6);
root ->
left ->
left = new TreeNode(3);
root ->
left ->
right = new TreeNode(1);
root ->
right ->
right = new TreeNode(5);
cout <<
"Original Tree (Level Order):\n";
printTreeByLevels(root);
int val = 1, depth = 2;
root = insertRow(root, val, depth);
cout <<
"\nTree After Adding Row (Level Order):\n";
printTreeByLevels(root);
return 0;
}
Below is the output of the above program, which displays the tree's level order traversal before and after adding the new row:
Original Tree (Level Order): 4 2 6 3 1 5 Tree After Adding Row (Level Order): 4 1 1 2 6 3 1 5
Time Complexity: O(n) because we visit each node once during level order traversal.
Space Complexity: O(w) because the queue stores nodes level by level, and w is the maximum width of the tree.
Depth First Search (DFS)
To add a new row at a given depth, we use Depth First Search (DFS). DFS goes deep into each path of the tree before moving to the next one, using recursion. We continue going down each path until we reach depth-1 - 1. At that point, we insert the new nodes with the given value.
Algorithm
The following is an algorithm:
- First, we check if the given depth is 1. If it is, we create a new root node with the given value and make the original tree its left child. This handles the base case.
- If the depth is more than 1, we define a recursive function that accepts the current node and the current depth as arguments.
- In each recursive call, we check if the current node is null. If it is, we return back.
- If the current depth is one less than the given depth, we create two new nodes with the given value.
- Then, we attach the original left subtree under the new left node, and the original right subtree under the new right node. After that, we set these new nodes as the left and right children of the current node.
Example
Here is the C++ program to add a new row to a binary tree at the given depth using depth-first search:
#include<iostream>
#include<queue>
using namespace std;
// Definition of a tree node
struct TreeNode {
int value;
TreeNode* leftChild;
TreeNode* rightChild;
TreeNode(int data) : value(data), leftChild(NULL), rightChild(NULL) {}
};
// Recursive function to insert new row
void insertNewRow(TreeNode* currentNode, int newValue, int targetDepth, int currentDepth) {
if (currentNode == NULL) return;
// If we're at the level just above the target depth
if (currentDepth == targetDepth - 1) {
TreeNode* oldLeft = currentNode->leftChild;
TreeNode* oldRight = currentNode->rightChild;
currentNode->leftChild = new TreeNode(newValue);
currentNode->leftChild->leftChild = oldLeft;
currentNode->rightChild = new TreeNode(newValue);
currentNode->rightChild->rightChild = oldRight;
return;
}
// Recur for left and right subtrees
insertNewRow(currentNode->leftChild, newValue, targetDepth, currentDepth + 1);
insertNewRow(currentNode->rightChild, newValue, targetDepth, currentDepth + 1);
}
// Function to start adding a new row
TreeNode* addRowToTree(TreeNode* rootNode, int newValue, int rowDepth) {
if (rowDepth == 1) {
TreeNode* newRoot = new TreeNode(newValue);
newRoot->leftChild = rootNode;
return newRoot;
}
insertNewRow(rootNode, newValue, rowDepth, 1);
return rootNode;
}
// Function to print tree level by level
void printTreeByLevels(TreeNode* rootNode) {
if (!rootNode) return;
queue<TreeNode*> nodeQueue;
nodeQueue.push(rootNode);
while (!nodeQueue.empty()) {
int levelSize = nodeQueue.size();
while (levelSize--) {
TreeNode* currentNode = nodeQueue.front();
nodeQueue.pop();
cout << currentNode->value << " ";
if (currentNode->leftChild) nodeQueue.push(currentNode->leftChild);
if (currentNode->rightChild) nodeQueue.push(currentNode->rightChild);
}
cout << endl;
}
}
int main() {
// Creating the binary tree
TreeNode* root = new TreeNode(4);
root->leftChild = new TreeNode(2);
root->rightChild = new TreeNode(6);
root->leftChild->leftChild = new TreeNode(3);
root->leftChild->rightChild = new TreeNode(1);
root->rightChild->leftChild = new TreeNode(5);
int valueToAdd = 1;
int insertDepth = 2;
cout << "Original Tree (Level Order):\n";
printTreeByLevels(root);
// Add the new row
root = addRowToTree(root, valueToAdd, insertDepth);
cout << "\nTree After Adding Row (Level Order):\n";
printTreeByLevels(root);
return 0;
}
The output below shows the level order traversal of the tree before and after inserting the new row.
Original Tree (Level Order): 4 2 6 3 1 5 Tree After Adding Row (Level Order): 4 1 1 2 6 3 1 5
Time Complexity: O(n), because we visit each node exactly once.
Space Complexity: O(h), because the recursion stack depends on the tree's height.
Conclusion
In this article, we learned how to add a new row to a binary tree at a given depth using depth-first search(DFS) and breadth-first search(BFS). DFS uses recursion, while BFS uses a queue to reach the given depth. Both methods are efficient with O(n) time and space complexity.

