
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
AA Trees in C/C++?
An AA tree in computer science is defined as a form of balanced tree implemented for storing and retrieving ordered data efficiently. AA trees are treated as a variation of the red-black tree, a form of binary search tree which supports efficient addition and deletion of entries. As opposed to red-black trees, red nodes on an AA tree can only be added as a right subchild, no left subchild. The result of this operation is the simulation of a 2-3 tree instead of a 2-3-4 tree, which causes simplification the maintenance operations. The maintenance algorithms for a red-black tree require to assume or consider seven different shapes to properly balance the tree −
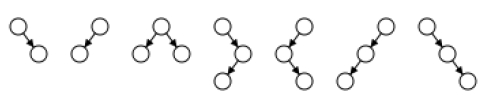
As opposed to red-black tree, an AA tree on the other hand only requires to assume or consider two shapes due to the strict requirement that only right links can be red −
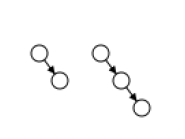
Balancing rotations
Whereas red-black trees need one bit of balancing metadata per node (the color), AA trees need O(log(log(N))) bits of metadata per node, in the form of an integer "level". The below invariants hold for AA trees −
The level of every leaf node is treated as one.
The level of every left child is exactly one smaller than that of its parent.
The level of every right child is equal to or one smaller than that of its parent.
The level of every right grandchild is strictly smaller than that of its grandparent.
Every node of level higher than one has two children.
Re-balancing an AA tree is procedurally much easier or simpler than re-balancing a red-black tree.
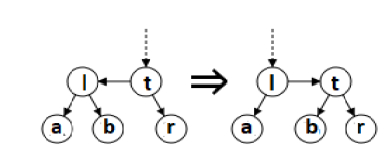
In case of an AA tree only two distinct operations are required for restoring balance: "skew" and "split". Skew is treated as a right rotation to replace a subtree consisting of a left horizontal link with one consisting of a right horizontal link instead. In case of Split, it is a left rotation and level increase to replace a subtree consisting two or more consecutive right horizontal links with one containing two fewer consecutive right horizontal links. The operations, "skew" and "split" , are explained below −
function skew is
input: An AA tree that needs to be rebalanced is represented by a node, t. output: The rebalanced AA tree is represented by another node. if nil(t) then return nil else if nil(left(t)) then return t else if level(left(t)) == level(t) then Exchange the pointers of horizontal left links. l = left(t) left(t) := right(l) right(l) := t return l else return t end if end function
function split is
input: An AA tree that needs to be rebalanced is represented by a node, t. output: The rebalanced AA tree is represented by another node. if nil(t) then return nil else if nil(right(t)) or nil(right(right(t))) then return t else if level(t) == level(right(right(t))) then We have two horizontal right links. The middle node is taken, elevate it, and return it. r = right(t) right(t) := left(r) left(r) := t level(r) := level(r) + 1 return r else return t end if end function
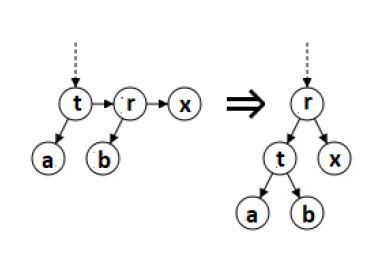
Split −

