
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHPPhysics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
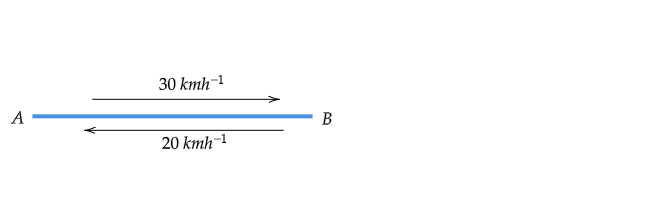
A motorcyclist drives from A to B with a uniform speed of $30\ kmh^{-1}$ and returns back with a speed of $20\ kmh^{-1}$. Find its average speed.
Let $D$ be the distance from $A$ to $B$.
As given, Speed of the motorcyclist from $A$ to $B$ $v_1=30\ kmh^{-1}$
Therefore, time taken from $A$ to $B$ $t_1=\frac{distance}{speed}=\frac{d}{30}\ h$
And also given, speed from $B$ to $A$ $v_2= 20\ km h^{-1}$
Therefore, time taken in return $t_2=\frac{d}{v_2}=\frac{d}{20}\ h$
Therefore, total distance travelled $=d+d=2d$
Total time taken $t_1+t_2=\frac{d}{30}+\frac{d}{20}=\frac{50d}{600}=\frac{d}{12}$
Therefore, average speed $=\frac{total\ distance}{total\ time}$
$=\frac{2d}{\frac{d}{12}}$
$=\frac{2d\times12}{d}$
$=24\ kmh^{-1}$
There, the average speed of the motorcyclist is $24\ kmh^{-1}$

Advertisements
