
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Selection Sort Algorithm
Selection sort is a simple sorting algorithm. This sorting algorithm, like insertion sort, is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.
The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundaries by one element to the right.
This algorithm is not suitable for large data sets as its average and worst case complexities are of O(n2), where n is the number of items.
Selection Sort Algorithm
This type of sorting is called Selection Sort as it works by repeatedly sorting elements. That is: we first find the smallest value in the array and exchange it with the element in the first position, then find the second smallest element and exchange it with the element in the second position, and we continue the process in this way until the entire array is sorted.
1. Set MIN to location 0. 2. Search the minimum element in the list. 3. Swap with value at location MIN. 4. Increment MIN to point to next element. 5. Repeat until the list is sorted.
Pseudocode
Algorithm: Selection-Sort (A)
fori← 1 to n-1 do
min j ←i;
min x ← A[i]
for j ←i + 1 to n do
if A[j] < min x then
min j ← j
min x ← A[j]
A[min j] ← A [i]
A[i] ← min x
Analysis
Selection sort is among the simplest of sorting techniques and it works very well for small files. It has a quite important application as each item is actually moved at the most once.
Section sort is a method of choice for sorting files with very large objects (records) and small keys. The worst case occurs if the array is already sorted in a descending order and we want to sort them in an ascending order.
Nonetheless, the time required by selection sort algorithm is not very sensitive to the original order of the array to be sorted: the test if [] < A[j] < min x is executed exactly the same number of times in every case.
Selection sort spends most of its time trying to find the minimum element in the unsorted part of the array. It clearly shows the similarity between Selection sort and Bubble sort.
Bubble sort selects the maximum remaining elements at each stage, but wastes some effort imparting some order to an unsorted part of the array.
Selection sort is quadratic in both the worst and the average case, and requires no extra memory.
For each i from 1 to n - 1, there is one exchange and n - i comparisons, so there is a total of n - 1 exchanges and
(n 1) + (n 2) + ...+2 + 1 = n(n 1)/2 comparisons.
These observations hold, no matter what the input data is.
In the worst case, this could be quadratic, but in the average case, this quantity is O(n log n). It implies that the running time of Selection sort is quite insensitive to the input.
Example
Consider the following depicted array as an example.
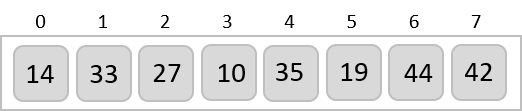
For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value.
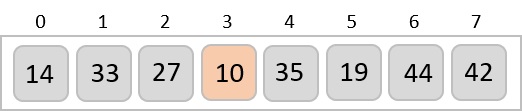
So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list.
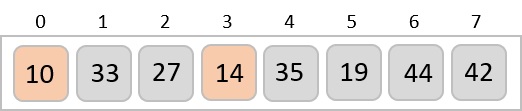
For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner.
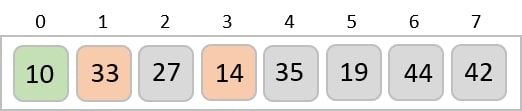
We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values.
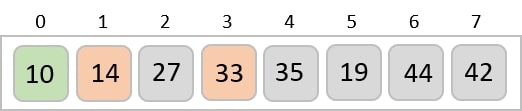
After two iterations, two least values are positioned at the beginning in a sorted manner.
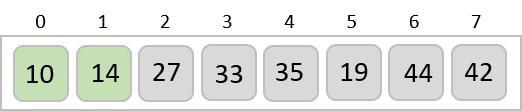
The same process is applied to the rest of the items in the array −
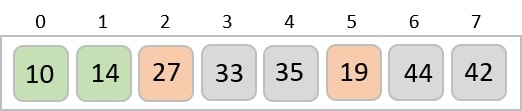
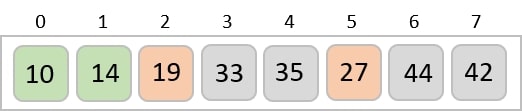
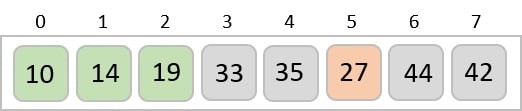
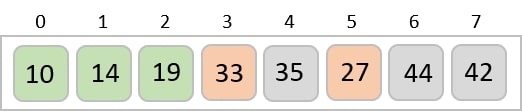
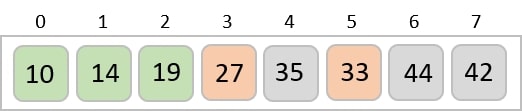
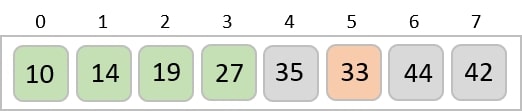
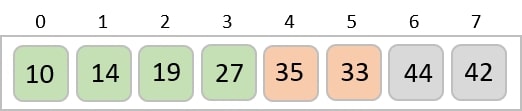
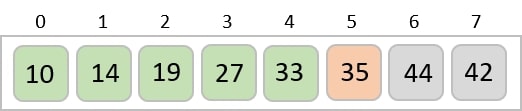
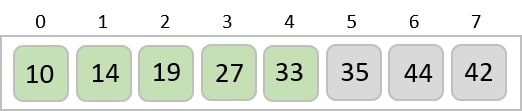
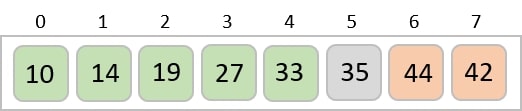
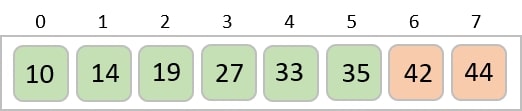

Implementation
The selection sort algorithm is implemented in four different programming languages below. The given program selects the minimum number of the array and swaps it with the element in the first index. The second minimum number is swapped with the element present in the second index. The process goes on until the end of the array is reached.
#include <stdio.h>
void selectionSort(int array[], int size){
int i, j, imin;
for(i = 0; i<size-1; i++) {
imin = i; //get index of minimum data
for(j = i+1; j<size; j++)
if(array[j] < array[imin])
imin = j;
//placing in correct position
int temp;
temp = array[i];
array[i] = array[imin];
array[imin] = temp;
}
}
int main(){
int n;
n = 5;
int arr[5] = {12, 19, 55, 2, 16}; // initialize the array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("\n");
selectionSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("\n");
}
Output
Array before Sorting: 12 19 55 2 16 Array after Sorting: 2 12 16 19 55
#include<iostream>
using namespace std;
void swapping(int &a, int &b) { //swap the content of a and b
int temp;
temp = a;
a = b;
b = temp;
}
void selectionSort(int *array, int size){
int i, j, imin;
for(i = 0; i<size-1; i++) {
imin = i; //get index of minimum data
for(j = i+1; j<size; j++)
if(array[j] < array[imin])
imin = j;
//placing in correct position
swap(array[i], array[imin]);
}
}
int main(){
int n;
n = 5;
int arr[5] = {12, 19, 55, 2, 16}; // initialize the array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
selectionSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}
Output
Array before Sorting: 12 19 55 2 16 Array after Sorting: 2 12 16 19 55
import java.io.*;
public class SelectionSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {12, 19, 55, 2, 16}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
int imin;
for(int i = 0; i<n-1; i++) {
imin = i; //get index of minimum data
for(int j = i+1; j<n; j++)
if(arr[j] < arr[imin])
imin = j;
//placing in correct position
int temp;
temp = arr[i];
arr[i] = arr[imin];
arr[imin] = temp;
}
System.out.print("Array After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Array before Sorting: 12 19 55 2 16 Array After Sorting: 2 12 16 19 55
def insertion_sort(array, size):
for i in range(size):
imin = i
for j in range(i+1, size):
if arr[j] < arr[imin]:
imin = j
temp = array[i];
array[i] = array[imin];
array[imin] = temp;
arr = [12, 19, 55, 2, 16]
n = len(arr)
print("Array before Sorting: ")
print(arr)
insertion_sort(arr, n);
print("Array after Sorting: ")
print(arr)
Output
Array before Sorting: [12, 19, 55, 2, 16] Array after Sorting: [2, 12, 16, 19, 55]
