Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum size square submatrix with all 1s
When a binary matrix is given, our task is to find a square matrix whose all elements are 1.
For this problem, we will make an auxiliary size matrix, whose order is the same as the given matrix. This size matrix will help to represent, in each entry Size[i, j], is the size of a square matrix with all 1s. From that size matrix, we will get the maximum number to get the size of the biggest square matrix.
Input and Output
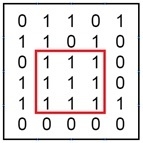
Input: The binary matrix. 0 1 1 0 1 1 1 0 1 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 0 Output: The largest submatrix with all 1’s.
Algorithm
subMatWithOne(given matrix)
Input − The main matrix.
Output − Display the square matrix with all 1, which one is the largest.
Begin define subMat whose order is same as given matrix copy first row and first column of given matrix to subMat for all row i (1 to n), do for all column j (1 to n), do if matrix[i, j] = 1, then subMat[i, j] := 1 + minimum of subMat[i, j-1] and subMat[i-1, j-1] else subMat[i, j] := 0 done done maxSize := subMat[0, 0], iMax := 0 and jMax := 0 for all row i and column j, do if maxSize < subMat[i, j], then maxSize := subMat[i, j] iMax := i, jMax := j done print sub matrix from row = iMax to (iMax - maxSize), and column jMax to (jMax - maxSize) End
Example
#include<iostream>
#define ROW 6
#define COL 5
using namespace std;
int matrix[ROW][COL] = {
{0, 1, 1, 0, 1},
{1, 1, 0, 1, 0},
{0, 1, 1, 1, 0},
{1, 1, 1, 1, 0},
{1, 1, 1, 1, 1},
{0, 0, 0, 0, 0}
};
int min(int a, int b, int c) {
return ((a<b?a:b))?((a<c)?a:c):((b<c)?b:c);
}
void subMatWithOne() {
int subMat[ROW][COL];
int maxSize, iMax, jMax;
for(int i = 0; i < ROW; i++) //copy first row of matrix to sub matrix
subMat[i][0] = matrix[i][0];
for(int j = 0; j < COL; j++) //copy first column of matrix to sub matrix
subMat[0][j] = matrix[0][j];
for(int i = 1; i < ROW; i++) {
for(int j = 1; j < COL; j++) {
if(matrix[i][j] == 1) //find minimum of left, top and diagonal element + 1
subMat[i][j] = min(subMat[i][j-1], subMat[i-1][j], subMat[i-1][j-1]) + 1;
else
subMat[i][j] = 0; //if item is 0, put only 0
}
}
maxSize = subMat[0][0]; iMax = 0; jMax = 0;
for(int i = 0; i < ROW; i++) { //find the order of sub square matrix
for(int j = 0; j < COL; j++) {
if(maxSize < subMat[i][j]) {
maxSize = subMat[i][j];
iMax = i;
jMax = j;
}
}
}
cout << "Subsquare matrix: "<<endl;
for(int i = iMax; i > iMax - maxSize; i--) { //print the submatrix using max size
for(int j = jMax; j > jMax - maxSize; j--) {
cout << matrix[i][j]<<" ";
}
cout << endl;
}
}
int main() {
subMatWithOne();
} Output
Subsquare matrix: 1 1 1 1 1 1 1 1 1
Updated on: 17-Jun-2020
201 Views
Advertisements