Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print maximum sum square sub-matrix of given size in C Program.
Given a matrix of NxN find a sub matrix of MxM where M<=N and M>=1 such that addition of all the elements of matrix MxM is maximum. Input of matrix NxN can contain zero, positive and negative integer values.
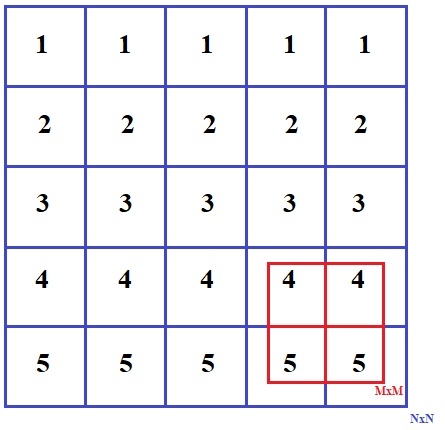
Example
Input:
{{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5} }
Output:
4 4
5 5The above problem can be solved by a simple solution in which we can take whole matrix NxN, then find out all possible MxM matrix and find their sum, then print the one matrix of MxM with the maximum sum. This approach is easy but require O(N^2.M^2) time complexity, so we try to find out a way which takes less time complexity.
Algorithm
Start Step 1 -> Declare Function void matrix(int arr[][size], int k) IF k>size Return Declare int array[size][size] Loop For int j=0 and j<size and j++ Set sum=0 Loop for int i=0 and i<k and i++ Set sum=sum + arr[i][j] End Set array[0][j]=sum Loop For int i=1 and i<size-k+1 and i++ Set sum=sum+(arr[i+k-1]][j]-arr[i-1][j] Set arrayi][j]=sum End Set int maxsum = INT_MIN and *pos = NULL Loop For int i=0 and i<size-k+1 and i++) Set int sum = 0 Loop For int j = 0 and j<k and j++ Set sum += array[i][j] End If sum > maxsum Set maxsum = sum Set pos = &(arr[i][0]) End Loop For int j=1 and j<size-k+1 and j++ Set sum += (array[i][j+k-1] - array[i][j-1]) IF sum > maxsum Set maxsum = sum Set pos = &(arr[i][j]) End End End Loop For int i=0 and i<k and i++ Loop For int j=0 and j<k and j++ Print *(pos + i*size + j) End Print
End Step 2 -> In main() Declare int array[size][size] = {{1, 1, 1, 1, 1}, {2, 2, 2, 2, 2}, {3, 3, 3, 3, 3}, {4, 4, 4, 4, 4}, {5, 5, 5, 5, 5}} Declare int k = 2 Call matrix(array, k) Stop
Example
#include <bits/stdc++.h>
using namespace std;
#define size 5
void matrix(int arr[][size], int k){
if (k > size) return;
int array[size][size];
for (int j=0; j<size; j++){
int sum = 0;
for (int i=0; i<k; i++)
sum += arr[i][j];
array[0][j] = sum;
for (int i=1; i<size-k+1; i++){
sum += (arr[i+k-1][j] - arr[i-1][j]);
array[i][j] = sum;
}
}
int maxsum = INT_MIN, *pos = NULL;
for (int i=0; i<size-k+1; i++){
int sum = 0;
for (int j = 0; j<k; j++)
sum += array[i][j];
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][0]);
}
for (int j=1; j<size-k+1; j++){
sum += (array[i][j+k-1] - array[i][j-1]);
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][j]);
}
}
}
for (int i=0; i<k; i++){
for (int j=0; j<k; j++)
cout << *(pos + i*size + j) << " ";
cout << endl;
}
}
int main(){
int array[size][size] = {
{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5},
};
int k = 2;
matrix(array, k);
return 0;
}Output
if we run above program then it will generate following output
4 4 5 5
Updated on: 22-Aug-2019
448 Views
Advertisements