
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
8085 program to find square root of a number
Now let us see a program of Intel 8085 Microprocessor. This program will find the square root of a number.
Problem Statement
Write an assembly language program to find the square root of a number in L and store the result at location 8100H
Discussion
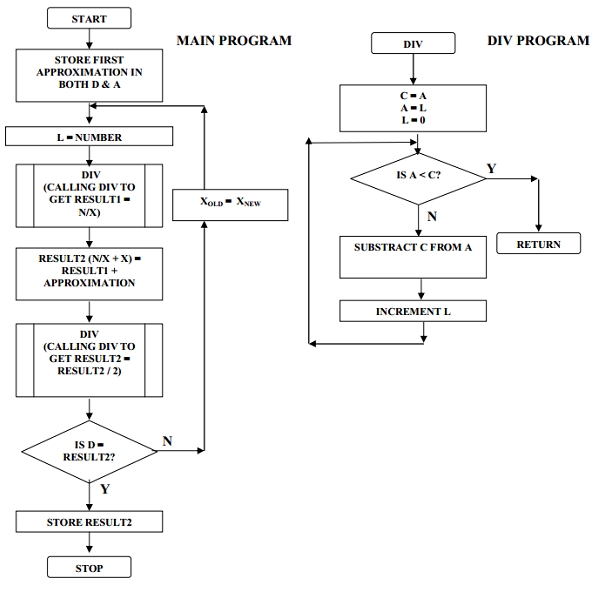
Here we are using division method for finding square root of a number. As we know there is no division operation in 8085, so we are creating division subroutine.
Let N is the number.
X = √N
X2 = N
X2 + X2 = N + X2
2X2 = N + X2
X2 = (N + X2)/2
X =((N + X2)/X)/2
XNew=(N / X + X)/2
If X = XNew then X = √N
Input
We have tested with three inputs: These inputs are −
- 64H (100D)
- 51H (81D)
- 90H (144D)
Flow Diagram
Program
| Address |
HEX Codes |
Labels |
Mnemonics |
Comments |
|---|---|---|---|---|
| 8000 |
80, 00, 83 |
START |
LXI SP, 8300H |
SP = 8300H |
| 8003 |
3E, 01 |
MVI A, 01H |
A (first approximation) = 01 H |
|
| 8005 |
57 |
UP |
MOV D, A |
D = A Tracking Xold |
| 8006 |
2E, NUM |
MVI L, NUM |
L = number N whose square root is to be calculated |
|
| 8008 |
CD, 1E, 80 |
CALL DIV |
Call div subroutine to calculate N/X HereN in L and X in A. It performs L = L/A and it returns result in L |
|
| 800B |
7D |
MOV A, L |
A = L (return argument) |
|
| 800C |
82 |
ADD D |
A = A+D (N/X) + X |
|
| 800D |
26, 00 |
MVI H, 00H |
H = 00 H |
|
| 800F |
6F |
MOV L, A |
L = A |
|
| 8010 |
3E, 02 |
MVI A, 02H |
A = 02 H |
|
| 8012 |
CD, 1E, 80 |
CALL DIV |
Call div subroutine Here sum in L and 2in A Xnew= ((N/Xold)+ Xold)/2 |
|
| 8015 |
7D |
MOV A, L |
A = L |
|
| 8016 |
BA |
CMP D |
Compare D and A Comparing Xold and Xnew |
|
| 8017 |
C2, 05, 80 |
JNZ UP |
Is A = D, if no go to up If they are equal then the obtained value of X is the answer |
|
| 801A |
32, 00, 81 |
STA 8100H |
Store the result at the desired memory location 8100H |
|
| 801D |
76 |
HLT |
Stop |
|
| 801E |
4F |
DIV |
MOV C, A |
C = A |
| 801F |
7D |
MOV A, L |
A = l |
|
| 8020 |
2E, 00 |
MVI L, 00H |
L = 00 |
|
| 8022 |
B9 |
UP1 |
CMP C |
Compare a and c registers |
| 8023 |
D8 |
RC |
Is A < C? If yes return to main |
|
| 8024 |
91 |
SUB C |
A = A – C |
|
| 8025 |
2C |
INR L |
L = L + 1 |
|
| 8026 |
C3, 22, 80 |
JMP UP1 |
Go back to UP1 |
|
| 8000 |
80, 00, 83 |
START |
LXI SP, 8300H |
SP = 8300H |
Output
first output
| Address |
Data |
|---|---|
| . . . |
. . . |
| 8100 |
0A |
| . . . |
. . . |
second output
| Address |
Data |
|---|---|
| . . . |
. . . |
| 8100 |
09 |
| . . . |
. . . |
third output
| Address |
Data |
|---|---|
| . . . |
. . . |
| 8100 |
0C |
| . . |
. . . |

Advertisements
