Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
ZigZag Tree Traversal in C++
In this problem, we are given a binary tree. Our task is to print the binary tree in a zigzag form.
Let’s take an example to understand the problem,
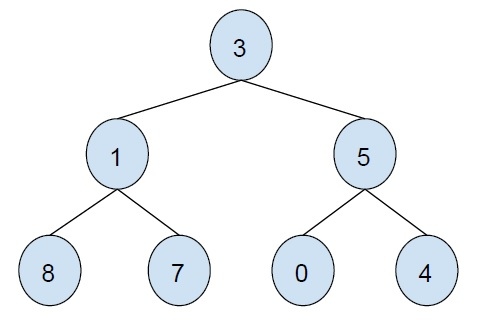
The zigzag traversal of the above binary tree is
3 5 1 8 7 0 4
To solve this problem, we need to traverse the binary tree level by level. The order of traversal will be flipped after each level.
Now, we will use two stacks(current and next) and one value for order. First, we will traverse the node from current and feed nodes from the left child to the right child so that reverse order will be returned. The again reverse from the current. The order variable plays a vital role in showing which side is to be printed.
Example
Program to show the implementation of our solution,
#include <iostream>
#include <stack>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
void zigZagTreeTraversal(struct Node* root){
if (!root)
return;
stack<struct Node*> currentlevel;
stack<struct Node*> nextlevel;
currentlevel.push(root);
bool LtR = true;
while (!currentlevel.empty()) {
struct Node* temp = currentlevel.top();
currentlevel.pop();
if (temp) {
cout<<temp->data<<"\t";
if (LtR) {
if (temp->left)
nextlevel.push(temp->left);
if (temp->right)
nextlevel.push(temp->right);
}
else {
if (temp->right)
nextlevel.push(temp->right);
if (temp->left)
nextlevel.push(temp->left);
}
}
if (currentlevel.empty()) {
LtR = !LtR;
swap(currentlevel, nextlevel);
}
}
}
struct Node* insertNode(int data){
struct Node* node = new struct Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main() {
struct Node* root = insertNode(3);
root->left = insertNode(1);
root->right = insertNode(5);
root->left->left = insertNode(8);
root->left->right = insertNode(7);
root->right->left = insertNode(0);
root->right->right = insertNode(4);
cout << "ZigZag traversal of the given binary tree is \n";
zigZagTreeTraversal(root);
return 0;
}Output
ZigZag traversal of the given binary tree is 3 5 1 8 7 0 4
Updated on: 17-Apr-2020
377 Views
Advertisements