Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is algorithm for computing the CRC?
Cyclic Redundancy Check (CRC)
Cyclic Redundancy Check (CRC) is a block code that was invented by W. Wesley Peterson in 1961. It is commonly used to detect accidental changes to data transmitted via telecommunications networks and storage devices.
CRC involves binary division of the data bits being sent by a predetermined divisor agreed upon by the communicating system. The divisor is generated using polynomials. So, CRC is also called polynomial code checksum.
Before sending the message over network channels, the sender encodes the message using CRC. The receiver decodes the incoming message to detect error. If the message is error-free, then it is accepted, otherwise, the receiver asks for re-transmission of the message.
The process is illustrated as follows:
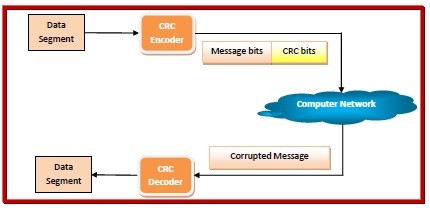
Computation of CRC
When messages are encoded using CRC (polynomial code), a fixed polynomial called generator polynomial,𝐺G(x) is used. The value of is mutually agreed upon by the sending and the receiving parties. A k – bit word is represented by a polynomial which ranges from X0 to xk-1. The order of this polynomial is the power of the highest coefficient, i.e.(K-1) The length of G(x) should be less than the length of the message it encodes. Also, both its MSB (most significant bit) and LSB (least significant bit) should be 1. In the process of encoding, CRC bits are appended to the message so that the resultant frame is divisible by G(x).
Algorithm for Encoding using CRC
The communicating parties agrees upon the size of message,M(x) and the generator polynomial, G(x).
If r is the order of G(x),r, bits are appended to the low order end of M(x). This makes the block size bits, the value of which is xrM(x).
The block xrM(x) is divided by G(x) using modulo 2 division.
The remainder after division is added to xrM(x) using modulo 2 addition. The result is the frame to be transmitted, T(x). The encoding procedure makes exactly divisible by G(x).
Algorithm for Decoding using CRC
The receiver divides the incoming data frame T(x) unit by G(x) using modulo 2 division. Mathematically, if E(x) is the error, then modulo 2 division of [M(x) + E(x)] by G(x) is done.
If there is no remainder, then it implies that E(x). The data frame is accepted.
A remainder indicates a non-zero value of E(x), or in other words presence of an error. So the data frame is rejected. The receiver may then send an erroneous acknowledgment back to the sender for retransmission.
5K+ Views
