Ways to place items in n^2 positions such that no row/column contains more than one in C++

In this problem, we are given an integer n such that there are n lines vertically and n horizontally that are placed such that there are n2 intersection between these lines. Our task is to find the total number of ways by which 4 items can be placed on these intersections in

such a way that no row and column contains more that one item.

Let’s take an example to understand the problem,

Input

n=4

Output

24

Explanation

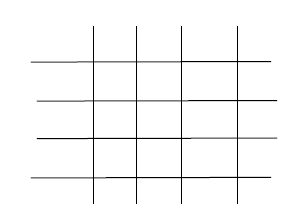
To solve this problem, we will have to choose 4 horizontal lines from n lines that will have items which will be nC4. Now, every horizontal line has n vertical lines so, there will be n way to place an item in the first selected horizontal line. Then, we will move to the next selected horizontal line where there will be n-1 possible placements. And it the same way third could be placed in n-2 and forth in n-3 ways. So, the total number of wats will be ⁿC4*n*(n-1)*(n-2)*(n-3)

Program to show the implementation of the algorithm,

Example

 Live Demo

#include <iostream>
using namespace std;
long long placeItems(int n) {
   return (1LL * (1LL *
   ((n) * (n - 1) * (n - 2) * (n - 3)) / (4 * 3 * 2 * 1)) *
   ((1LL * (n) * (n - 1) * (n - 2) * (n - 3))));
}
int main() {
   int n = 4;
   cout<<"The number of way is which 4 items can be placed in the intersection of "<<n;
   cout<<" lines vertically and horizotally are "<<placeItems(n);
   return 0;
}

Output

The number of way is which 4 items can be placed in the intersection of 4 lines vertically and horizotally are 24