Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Time Needed to Inform All Employees in C++
Suppose we have a company has n employees with a unique ID for each employee. These IDs are ranging from 0 to n - 1. The head of the company has is the one with headID. Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also it's guaranteed that the subordination relationships have a tree-like structure. Here the head of the company wants to inform all the employees of the company of an urgent piece of news. He can inform his direct subordinates and they will inform their subordinates and so on until all employees know about the urgent news. The i-th employee needs the informTime[i] minutes to inform all of his direct subordinates (So after informTime[i] minutes, all his direct subordinates can start spreading the news). We have to find the number of minutes needed to inform all the employees about the urgent news. So if the input is like n = 6, headID = 2, manager = [2,2,-1,2,2,2], infromTime = [0,0,1,0,0,0], then the output will be 1.
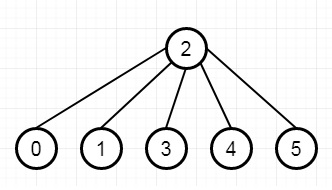
To solve this, we will follow these steps −
ret := 0
define an array called the graph of size n, set root := -1
for i in range 0 to the size of manager array
u := managet[i] and v := i
if u is -1, then set root := v, and go for next iteration
insert v into graph[u]
define a queue q, insert root into q, and define an array called time, of size n
until the q is not empty
curr := front element of q, and delete front element from q
if size of the list of graph[curr] is 0, then skip to the next iteration
for i in range 0 to the size of the list of graph[curr]
insert graph[curr, i] into q
time[graph[curr, i]] := time[curr] + informTime[curr]
for i in range 0 to n – 1: ret := max of ret and time[i]
return ret
Example (C++)
Let us see the following implementation to get a better understanding −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
int ret = 0;
vector <int> graph[n];
int root = -1;
for(int i = 0; i < manager.size(); i++){
int u = manager[i];
int v = i;
if(u == -1) {
root = v;
continue;
}
graph[u].push_back(v);
}
queue <int> q;
q.push(root);
vector <int> time(n);
while(!q.empty()){
int curr = q.front();
q.pop();
if(!graph[curr].size()) continue;
for(int i = 0; i < graph[curr].size(); i++){
q.push(graph[curr][i]);
time[graph[curr][i]] = time[curr] + informTime[curr];
}
}
for(int i = 0; i <n; i++)ret = max(ret, time[i]);
return ret;
}
};
main(){
vector<int> v = {2,2,-1,2,2,2}, v1 = {0,0,1,0,0,0};
Solution ob;
cout << (ob.numOfMinutes(6, 2, v, v1));
}Input
6 2 [2,2,-1,2,2,2] [0,0,1,0,0,0]
Output
1
376 Views
