The Realization of Logic Functions Using NAND Gates

A logic function is a basically a Boolean expression that returns a Boolean value, which is a value that is either TRUE or FALSE. The NAND gate is a universal logic gate, thus it can be used to implement any type of logic function. Read this tutorial to learn how you can realize different logic functions using NAND gates. Let's start with a basic introduction of the NAND gates

What is a NAND Gate?

A NAND Gate is a type of universal logic gate that one can use to realize any kind logical expression or any other type of logic gate. It is a combination of two basic logic gates namely AND gate and NOT gate, i.e.,

$$\mathrm{NAND\: Gate = AND \:Gate+NOT\:Gate}$$

Thus, NAND means NOT AND, i.e. AND operation NOTed. A NAND gate is the type of logic gate whose output is LOW (Logic 0) when all its inputs are high, and its output is HIGH (Logic 1), when any of its inputs is LOW (Logic 0). Therefore, the operation of the NAND gate is opposite that of the AND gate. The logic symbol of a two input NAND gate is shown in Figure-1.

The variables A and B are the inputs to the NAND gate and Y is the output variable of the NAND gate, then its output is given by,

$$\mathrm{Y = \overline{A\cdot B}=(A\cdot B)'}$$

It is read as “Y is equal to A.B whole bar”.

The operation of a NAND gate for different combinations of inputs can be understood with the help of the truth table of the NAND gate. The following is the truth table of the NAND gate −

Input		Output
A	B	Y = (A.B)'
0	0	1
0	1	1
1	0	1
1	1	0

Now, let us understand the realization of a logic function using NAND gates.

Implementation of Logic Function using NAND Gates

Like any other logic gate, the NAND gate can also be used to implement logic functions. The important point to remember about the NAND gate is that it performs the inverse operation of the basic AND gate. Therefore, the output of the NAND gate is equivalent to the complement of the output of the AND gate.

Now, let us understand the realization of logic functions using NAND gates with the help of examples. Consider a logic function of three variables,

$$\mathrm{F(A,B,C)=\bar{A}+(A+\bar{B})\cdot (A+B\bar{C})}$$

We have implement this logic function by using NAND gates only.

In the NAND gate implementation of a logic function, we use only NAND gates at input as well output sides of the logic circuit.

The step-by- step procedure for the realization of a logic function using NAND gates is shown below

Step 1

First, realize the given logic function using AND gates and OR Gates. The AND-OR realization of the given logic function is shown in Figure-2.

Step 2

Convert all the AND gates into NAND gates by introducing a bubble or complement at the output of each AND gate. But, in order to compensate the effect of bubble, the input of the next gate must be complemented by introducing a bubble. The implementation of AND with bubble at output is shown in Figure-3.

Step 3

Now, to maintain uniformity at the input, if a logic gate has one input with a bubble (complement), then the other input must also have a bubble. To compensate the effect of the bubble, the output of the preceding logic gate must be introduced with a bubble. This implementation is shown in Figure-4.

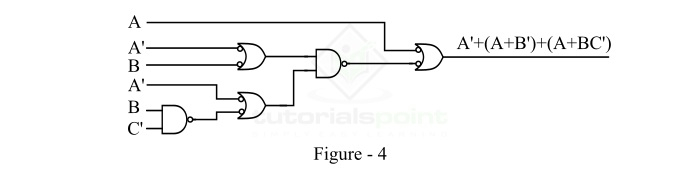
Step 4

According to the DeMorgan's Theorem, an OR gate with two bubbled inputs is equal to a NAND gate, i.e. A'+B' = (AB)'. Therefore, we can replace all the bubbled OR gate with NAND gates. By doing this, we get the final logic implementation of the given logic function using NAND gates only. This implementation is shown in Figure-5.

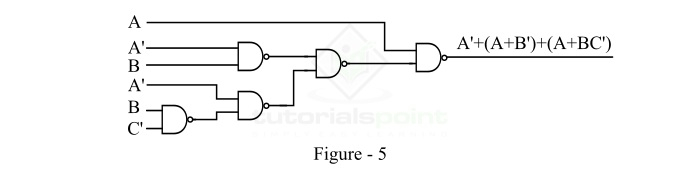
In this way, we can realize any logic (or Boolean) function using NAND gates only