Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
The Maze III in C++
Suppose there is a maze with empty spaces and walls and there is also a ball in that maze. The ball can go through empty spaces by rolling up (u), down (d), left (l) or right (r) directions, but it keeps rolling until hitting a wall. When the ball stops, it could choose the next direction. One hole is also in that maze. The ball will drop into the hole if it rolls on to the hole.
So if we have the ball position, the hole position and the maze, we have to find out how the ball could drop into the hole by moving the shortest distance. Here the distance is defined by the number of empty spaces traveled by the ball from the start (excluded) to the hole (included).
Return the moving directions by using 'u', 'd', 'l' and 'r'. Since there could be several different shortest ways, And the output should be lexicographically smallest way. If the ball cannot reach the hole, display "impossible".
Here the maze is represented by a binary matrix. 1 means the wall and 0 means the empty space. The ball and the hole coordinates are represented by row and column indexes.
So, if the input is like
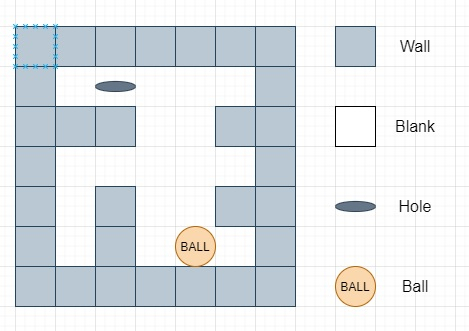
Then the output will be ‘lul’ as move left, then up then left, another outcome may be ‘ul’, up then left, both are of length 6, but that is not lexicographically smaller than ‘lul’
To solve this, we will follow these steps −
Define one data type called Data, this will take distance, a string d and coordinate x,y.
Define an array dir of size: 4 x 2 := {{1, 0}, {0, - 1}, {0, 1}, { - 1, 0}}
Define an array dirst of size: 4 := {'d', 'l', 'r', 'u'}
Define a function ok(), this will take x1, y1, x2, y2,
return true if x1 is same as x2 AND y1 is same as y2
From the main method do the following −
n := row size of maze
m := (if n is non-zero, then col size of maze, otherwise 0)
Define one priority queue pq
insert new data with (0, ball[0], ball[1], "") into pq
Define one 2D array visited of size n x m
while (not pq is empty), do −
curr := top element of pq
x := curr.x
y := curr.y
dist := curr.dist
d := curr.d
if ok(x, y, hole[0], hole[1]), then −
return d
visited[x, y] := true
delete element from pq
for initialize k := 0, when k − 4, update (increase k by 1), do −
nx := x, ny := y
tempDist := 0
while nx + dir[k, 0] < n and nx + dir[k, 0] >= 0 and ny + dir[k, 1] < m and ny + dir[k, 1] >= 0 and maze[nx + dir[k, 0], ny + dir[k, 1]] is 0, do −
nx := nx + dir[k, 0]
ny := ny + dir[k, 1]
(increase tempDist by 1)
if ok(nx, ny, hole[0], hole[1]), then −
Come out from the loop
if visited[nx, ny] is zero, then −
insert new Data(dist + tempDist, nx, ny, d + dirst[k]) into pq
return "impossible"
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
int dir[4][2] = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}};
char dirst[4] = {'d', 'l', 'r', 'u'};
class Solution {
public:
struct Data {
int dist;
string d;
int x, y;
Data(int a, int b, int c, string s) {
d = s;
dist = a;
x = b;
y = c;
}
};
struct Comparator {
bool operator()(Data a, Data b) {
return a.dist != b.dist ? !(a.dist < b.dist) : !(a.d < b.d);
}
};
bool ok(int x1, int y1, int x2, int y2) { return x1 == x2 && y1 == y2; }
string findShortestWay(vector<vector<int>> &maze, vector<int>&ball,
vector<int> &hole) {
int n = maze.size();
int m = n ? maze[0].size() : 0;
priority_queue<vector<Data>, vector<Data>, Comparator> pq;
pq.push(Data(0, ball[0], ball[1], ""));
vector<vector<bool>> visited(n, vector<bool>(m));
while (!pq.empty()) {
Data curr = pq.top();
int x = curr.x;
int y = curr.y;
int dist = curr.dist;
string d = curr.d;
if (ok(x, y, hole[0], hole[1])) {
return d;
}
visited[x][y] = true;
pq.pop();
for (int k = 0; k < 4; k++) {
int nx = x;
int ny = y;
int tempDist = 0;
while (nx + dir[k][0] < n && nx + dir[k][0] >= 0 && ny + dir[k][1] < m && ny + dir[k][1] >= 0 && !maze[nx + dir[k][0]][ny + dir[k][1]]) {
nx += dir[k][0];
ny += dir[k][1];
tempDist++;
if (ok(nx, ny, hole[0], hole[1]))
break;
}
if (!visited[nx][ny]) {
pq.push(Data(dist + tempDist, nx, ny, d + dirst[k]));
}
}
}
return "impossible";
}
};
main() {
Solution ob;
vector<vector<int>> v = {
{0, 0, 0, 0, 0},
{1, 1, 0, 0, 1},
{0, 0, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 1, 0, 0, 0}};
vector<int> v1 = {4, 3}, v2 = {0, 1};
cout << (ob.findShortestWay(v, v1, v2));
}Input
vector<vector<int>> v = {{0, 0, 0, 0, 0},
{1, 1, 0, 0, 1},
{0, 0, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 1, 0, 0, 0}};
vector<int> v1 = {4, 3}, v2 = {0, 1};Output
lul
367 Views
