Swift Program to Find the Area of a Parallelogram

This tutorial will discuss how to write a swift program to find the area of a parallelogram.A Parallelogram is a quadrilateral that is created using parallel lines.

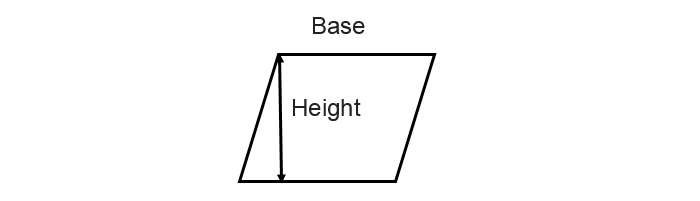
Where the opposite sides are parallel and equal and the opposite angles of the parallelograms are equal. It is of three types - rectangle, square, and rhombus.

In a parallelogram, an area is known as the space that is enclosed inside the boundaries or sides of the parallelogram in the two-dimensional plane. Suppose we have a tea try now the area of the parallelogram helps us to find how much paint we required to cover the top of the tea tray. We can calculate the area of the parallelogram using the following ways −

Using Height

Using the length of the sides

Using diagonals

Area of a parallelogram using height

We can calculate the area of the parallelogram with the help of height. Suppose we have P and Q as the set of the parallel sides and the distance between them is H. H is also known as the height of the parallelogram. So the area of the parallelogram is the product of the base and the height.

Formula

Following is the formula of the area of a parallelogram

Area = Base x Height
Or
Area = Q x H

Where Q is the base and H is the height of the parallelogram.

Algorithm to find Area of a Parallelogram using Height

• Step 1 − Define two variables for Base and Height

• Step 2 − Assign the value of those variables

• Step 3 − Implement Area of Parallelogram formula using height (Area = Base x Height)

• Step 4 − Print the output

Example

The following program shows how to calculate the area of the parallelogram with the help of height.

import Foundation
import Glibc

var base = 12
var height = 10

var AreaOfParallelogram = base * height

print("Base of the parallelogram:", base)
print("Height of the parallelogram:", height)
print("Final area of the parallelogram: ", AreaOfParallelogram)

Output

Base of the parallelogram: 12
Height of the parallelogram: 10
Final area of the parallelogram: 120

In the above code, we find the area of a parallelogram using the mathematical formula as shown in the below code −

var AreaOfParallelogram = base * height

Here the base of the parallelogram is 12 and the height of the parallelogram is 10. So the area of the parallelogram is 120.

Area of a parallelogram using sides

We can calculate the area of the parallelogram with the help of its adjacent sides and the angle between them. Suppose we have P and Q as the adjacent sides and O as the angle (ᶿ) between them in Radian. So the area of the parallelogram is the product of both the sides and the angle.

Formula

Following is the formula of the area of a parallelogram

Area = Side1 x Side2 x sin(ᶿ)
Or
Area = P x Q x sin(ᶿ)

Where P and Q are the lengths of the sides and O is the angle between them.

Algorithm to find Area of a Parallelogram using Sides

• Step 1 − Define three variables (Side 1, Side 2 and Angle)

• Step 2 − Assign the value of those variables

• Step 3 − Implement Area of Parallelogram formula using Sides (Area = Side1 x Side2 x sin(ᶿ))

• Step 4 − Print the output

Example

The following program shows how to calculate the area of the parallelogram with the help of sides.

import Foundation
import Glibc

var side1 = 12.0
var side2 = 10.0
var angle = 45.0

var AreaOfParallelogram = side1 * side2 * sin(angle * (Double.pi / 180.0))

print("Side 1 of the parallelogram:", side1)
print("Side 2 of the parallelogram:", side2)
print("Angle of the parallelogram:", angle)
print("Final area of the parallelogram: ", AreaOfParallelogram)

Output

Side 1 of the parallelogram: 12.0
Side 2 of the parallelogram: 10.0
Angle of the parallelogram: 45.0
Final area of the parallelogram: 84.85281374238569

In the above code, we find the area of a parallelogram using the mathematical formula as shown in the below code −

var AreaOfParallelogram = side1 * side2 * sin(angle * (Double.pi / 180.0))

Here, the two sides of the parallelogram are 12 and 10 and the angle is 45 degrees. So the area of the parallelogram is 84.85281374238569. In the code, we convert degree into radian using the below formula.

Radian = degrees *(Double.pi / 180.0)

Area of a parallelogram using diagonal

We can calculate the area of the parallelogram with the help of the diagonals. A parallelogram has two diagonals and they both intersect each other at some angle. Suppose we have two diagonals D1 and D2 and O is the angle between them in Radian. So the area of the parallelogram is the product of both the length of the diagonal and their angle.

Formula

Following is the formula of the area of a parallelogram −

Area = (Diagonal1 x Diagonal2 x sin(ᶿ))/2
Or
Area = (D1 x D2 x sin(O))/2

Where D1 and D2 are the lengths of the sides and O is the angle between them.

Algorithm to find Area of a Parallelogram using Diagonals

• Step 1 − Define three variables (Diagonal 1, Diagonal 2 and Angle)

• Step 2 − Assign the value of those variables

• Step 3 − Implement Area of Parallelogram formula using Diagonal (Area = (Diagonal1 x Diagonal2 x sin(ᶿ))/2)

• Step 4 − Print the output

Example

The following program shows how to calculate the area of the parallelogram with the help of diagonals.

import Foundation
import Glibc

var diagonal1 = 35.0
var diagonal2 = 40.0
var angle = 30.0
var AreaOfParallelogram = 1/2 * diagonal1 * diagonal2 * sin(angle * (Double.pi / 180.0))

print("Diagonal 1 of the parallelogram:", diagonal1)
print("Diagonal 2 of the parallelogram:", diagonal2)
print("Angle:", angle)
print("Final area of the parallelogram: ", AreaOfParallelogram)

Output

Diagonal 1 of the parallelogram: 35.0
Diagonal 2 of the parallelogram: 40.0
Angle: 30.0
Final area of the parallelogram: 349.99999999999994

In the above code, we find the area of a parallelogram using the mathematical formula as shown in the below code −

var AreaOfParallelogram = 1/2 * diagonal1 * diagonal2 * sin(angle * (Double.pi / 180.0))

Here, the two diagonals of the parallelogram are 35 and 40 and the angle is 30 degrees. So the area of the parallelogram is 349.99999999999994. In the code, we convert degree into radian using the below formula.

Radian = degrees *(Double.pi / 180.0)