Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Squirrel Simulation in C++
There's a tree, a squirrel, and several nuts. Positions are represented by the cells in a 2D grid. Your goal is to find the minimal distance for the squirrel to collect all the nuts and put them under the tree one by one. The squirrel can only take at most one nut at one time and can move in four directions - up, down, left, and right, to the adjacent cell. The distance is represented by the number of moves.
So, if the input is like Height: 5 Width: 7 Tree position: [2,2] Squirrel: [4,4] Nuts: [[3,0], [2,5]], then the output will be 12,
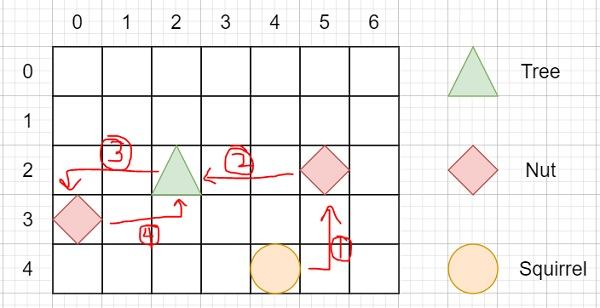
To solve this, we will follow these steps −
Define a function calc(), this will take x1, y1, x2, y2,
return |x1 - x2| + |y1 - y2|
Define a function minDistance(), this will take height, width, an array tree, an array sq, one 2D array nuts,
ret := 0
maxDiff := -inf
for initialize i := 0, when i < size of nuts, update (increase i by 1), do −
dist := calc(tree[0], tree[1], nuts[i, 0], nuts[i, 1])
ret := ret + 2 * dist
maxDiff := maximum of maxDiff and 2 * dist - (dist + calc(nuts[i, 0], nuts[i, 1], sq[0], sq[1]))
return ret - maxDiff
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int calc(int x1, int y1, int x2, int y2){
return abs(x1 - x2) + abs(y1 - y2);
}
int minDistance(int height, int width, vector<int>& tree, vector<int>& sq, vector<vector>& nuts) {
int ret = 0;
int maxDiff = INT_MIN;
for (int i = 0; i < nuts.size(); i++) {
int dist = calc(tree[0], tree[1], nuts[i][0],
nuts[i][1]);
ret += 2 * dist;
maxDiff = max(maxDiff, 2 * dist - (dist + calc(nuts[i][0], nuts[i][1], sq[0], sq[1])));
}
return ret - maxDiff;
}
};
main(){
Solution ob;
vector<int> v = {2,2}, v1 = {4,4};
vector<vector<int>> v2 = {{3,0}, {2,5}};
cout << (ob.minDistance(5,7,v, v1, v2));
}Input
5, 7, {2,2},{4,4}, {{3,0}, {2,5}}Output
12
208 Views
