Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Single-Source Shortest Paths, Nonnegative Weights
The single source shortest path algorithm (for non-negative weight) is also known Dijkstra algorithm. There is a given graph G(V,E) with its adjacency matrix representation, and a source vertex is also provided. Dijkstra’s algorithm to find the minimum shortest path between source vertex to any other vertex of the graph G.
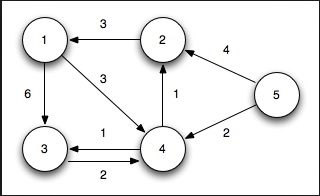
From starting node to any other node, find the smallest distances. In this problem the graph is represented using the adjacency matrix. (Cost matrix and adjacency matrix is similar for this purpose).
Input − The adjacency matrix −
0 3 6 ∞ ∞ ∞ ∞ 3 0 2 1 ∞ ∞ ∞ 6 2 0 1 4 2 ∞ ∞ 1 1 0 2 ∞ 4 ∞ ∞ 4 2 0 2 1 ∞ ∞ 2 ∞ 2 0 1 ∞ ∞ ∞ 4 1 1 0
Output −
0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7
Algorithm
dijkstraShortestPath(n, dist, next, start)
Input − Total number of nodes n, distance list for each vertex, next list to store which node comes next, and the seed or start vertex.
Output − The shortest paths from start to all other vertices.
Begin create a status list to hold the current status of the selected node for all vertices u in V do status[u] := unconsidered dist[u] := distance from source using cost matrix next[u] := start done status[start] := considered, dist[start] := 0 and next[start] := φ while take unconsidered vertex u as distance is minimum do status[u] := considered for all vertex v in V do if status[v] = unconsidered then if dist[v] > dist[u] + cost[u,v] then dist[v] := dist[u] + cost[u,v] next[v] := u done done End
Example(C++)
#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
{0, 3, 6, INF, INF, INF, INF},
{3, 0, 2, 1, INF, INF, INF},
{6, 2, 0, 1, 4, 2, INF},
{INF, 1, 1, 0, 2, INF, 4},
{INF, INF, 4, 2, 0, 2, 1},
{INF, INF, 2, INF, 2, 0, 1},
{INF, INF, INF, 4, 1, 1, 0}
};
int minimum(int *status, int *dis, int n){
int i, min, index;
min = INF;
for(i = 0; i<n; i++)
if(dis[i] < min && status[i] == 1){
min = dis[i];
index = i;
}
if(status[index] == 1)
return index;//minimum unconsidered vertex distance
else
return -1;//when all vertices considered
}
void dijkstra(int n, int *dist,int *next, int s){
int status[V];
int u, v;
//initialization
for(u = 0; u<n; u++){
status[u] = 1;//unconsidered vertex
dist[u] = costMat[u][s];//distance from source
next[u] = s;
}
//for source vertex
status[s] = 2; dist[s] = 0; next[s] = -1;//-1 for starting vertex
while((u = minimum(status, dist, n)) > -1){
status[u] = 2;//now considered
for(v = 0; v<n; v++)
if(status[v] == 1)
if(dist[v] > dist[u] + costMat[u][v]){
dist[v] = dist[u] + costMat[u][v];//update distance
next[v] = u;
}
}
}
main(){
int dis[V], next[V], i, start = 0;
dijkstra(V, dis, next, start);
for(i = 0; i<V; i++)
if(i != start)
cout << start << " to " << i <<", Using: " << next[i] << ", Cost: " << dis[i] << endl;
}Output
0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7
544 Views
