Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
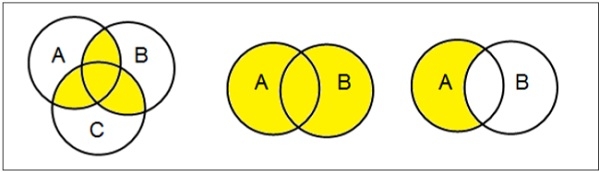
Set Operations
Venn diagram, invented in 1880 by John Venn, is a schematic diagram that shows all possible logical relations between different mathematical sets.
Examples
Set Operations
Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product.
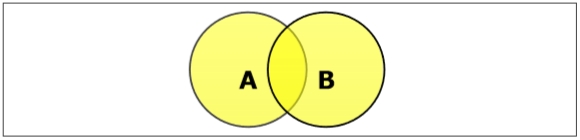
Set Union
The union of sets A and B (denoted by A ∪ B) is the set of elements that are in A, in B, or in both A and B. Hence, A ∪ B = { x | x ∈ A OR x ∈ B }.
Example − If A = { 10, 11, 12, 13 } and B = { 13, 14, 15 }, then A ∪ B = { 10, 11, 12, 13, 14, 15 }. (The common element occurs only once)
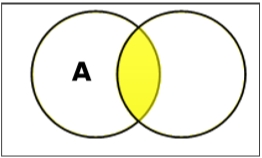
Set Intersection
The intersection of sets A and B (denoted by A ∩ B) is the set of elements which are in both A and B. Hence, A ∩ B = { x | x ∈ A AND x ∈ B }.
Example − If A = { 11, 12, 13 } and B = { 13, 14, 15 }, then A ∩ B = { 13 }.
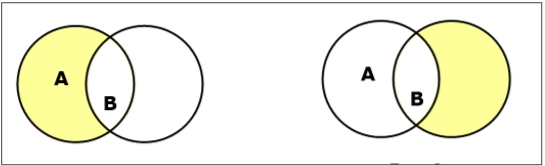
Set Difference/ Relative Complement
The set difference of sets A and B (denoted by A – B) is the set of elements that are only in A but not in B. Hence, A - B = { x | x ∈ A AND x ∉ B }.
Example − If A = { 10, 11, 12, 13 } and B = { 13, 14, 15 }, then (A - B) = { 10, 11, 12 } and (B - A) = { 14, 15 }. Here, we can see (A - B) ≠ (B - A)
Complement of a Set
The complement of a set A (denoted by A’) is the set of elements which are not in set A. Hence, A' = { x | x ∉ A }.
More specifically, A'= (U - A) where U is a universal set that contains all objects.
Example − If A = { x | x belongs to set of odd integers } then A' = { y | y does not belong to set of odd integers }
Cartesian Product / Cross Product
The Cartesian product of n number of sets A1, A2, ... An denoted as A1 × A2 ... × An can be defined as all possible ordered pairs (x1, x2, ... xn) where x1 ∈ A1, x2 ∈ A2, ... xn ∈ A_n
Example − If we take two sets A = { a, b } and B = { 1, 2 },
The Cartesian product of A and B is written as − A × B = { (a, 1), (a, 2), (b, 1), (b, 2)}
The Cartesian product of B and A is written as − B × A = { (1, a), (1, b), (2, a), (2, b)}
8K+ Views
