Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Rotation of a point about another point in C++
Rotation of a point X about origin is by an angle θ in anti-clockwise direction is done by −
X by θ about origin anti-clRotateockwise: X*polar( 1.0,θ ).
Here, the function polar for complex numbers is defined under <complex> header file and is used to find a complex number using phase angle and magnitude. polar(mag,angle) returns a complex number.
Rotation of point X about a point Y
To rotate a point about another point, we will use translation in which movement of all coordinates occur in a particular direction.
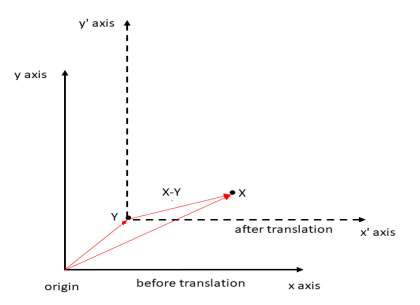
Steps to rotate X about Y.
Translate X to Y, so Y becomes the new origin. This can be done by subtracting Y from all points. X now becomes X-Y.
Rotate (X-Y) about new origin using above formula: (X-Y)*polar( 1.0,θ )
Back-translation by adding Y to all points.
Rotation of X about Y is : (X-Y)*polar( 1.0,θ ) + Y
Below is the code to demonstrate rotation of point about another point
Example
#include <iostream>
#include <complex>
using namespace std;
typedef complex<double> point;
#define x real()
#define y imag()
int main(){
// Rotate P about Q
point X(5.0, 3.0);
point Y(2.0, 4.0);
// Angle of rotation is 90 degrees
double theta = 3.14/2;
point Xnew=(X-Y) * polar(1.0, theta) + Y;
cout << "rotating X 90 degrees anti-clockwise about Y becomes:";
cout << "(" << Xnew.x << ", " << Xnew.y << ")" << endl;
return 0;
}Output
rotating X 90 degrees anti-clockwise about Y becomes:(3.00239, 6.9992)
874 Views
