Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Restoring Division Algorithm For Unsigned Integer in C++
Discuss dividing an unsigned integer using a division algorithm. Some division algorithms are applied on paper, and others are implemented on digital circuits. Division algorithms are of two types: slow division algorithm and fast division algorithm. Slow division algorithm includes restoring, non-performing restoring, SRT, and non-restoring algorithm.
In this tutorial, we will discuss the Restoring algorithm, assuming that 0 < divisor < dividend.
Approach to Find the Solution
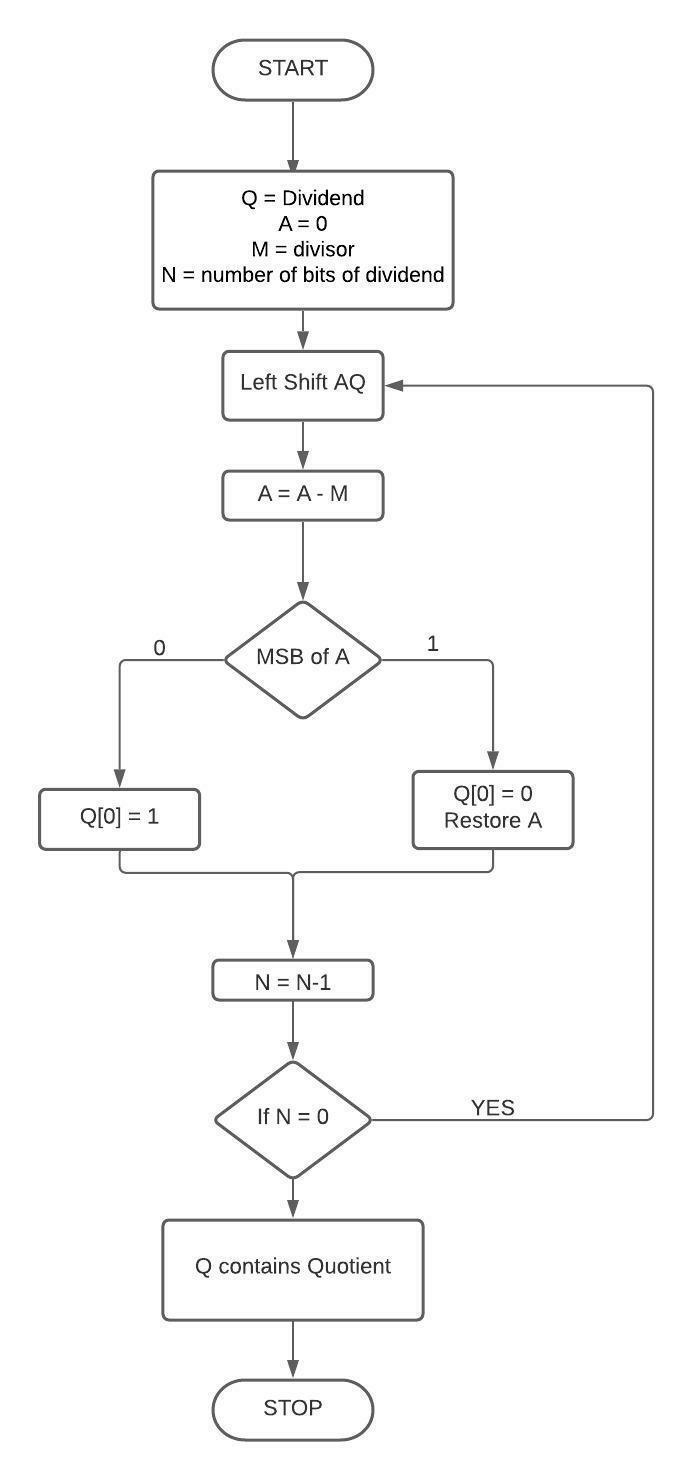
In this, we will use register Q to store quotient, register A to store remainder, and M to store divisor. The initial value of A is kept at 0, and its value is restored, which is why this method is restoring division.
Initialize registers with values,
Q = Dividend,
A = 0,
M = divisor,
N = number of bits of dividend.
Left shift AQ means taking register A and Q as a single unit.
Subtract A with M and store in A.
Check the most significant bit of A:
If it is 0, set the least significant bit to 1.
Else, set the least significant bit to 0.
Restore the value of A and decrement the value of counter N.
If N = 0, break the loop; otherwise, go to step 2.
The quotient is stored in register Q.
Flow Chart
Example
C++ Code for the Above Approach
#include <iostream>
using namespace std;
int main(){
// initializing all the variables with Dividend = 9, Divisor = 2.
int Q = 8,q=1,M=3;
short N = 4;
int A = Q;
M <<= N;
// loop for division by bit operation.
for(int i=N-1; i>=0; i--) {
A = (A << 1)- M;
// checking MSB of A.
if(A < 0) {
q &= ~(1 << i); // set i-th bit to 0
A = A + M;
} else {
q |= 1 << i; // set i-th bit to 1
}
}
cout << "Quotient: "<< q;
return 0;
}Output
Quotient: 2
Conclusion
In this tutorial, we discussed the Restoring division algorithm for an unsigned integer. We discussed a simple approach to solve this problem with the help of a flow chart and applying bit operations. We also discussed the C++ program for this problem which we can do with programming languages like C, Java, Python, etc. We hope you find this tutorial helpful.
1K+ Views
