Remove Edges Connected to a Node Such That The Three Given Nodes are in Different Trees Using C++

Suppose we are given a binary tree and three nodes in that binary. We have to disconnect one node entirely from the tree. Disconnecting that node leaves us with three different trees. Each of the three given nodes lies in one of them, or each of the given three nodes must not exist in the same tree.

Disconnecting a node means that we will remove all the edges from this node to all other nodes.

Example

For example, let's say we have a tree with three nodes 18, 15, and 17 as shown below −

If the task is to remove the node 12 we have to cut the links of this with the sub trees as:

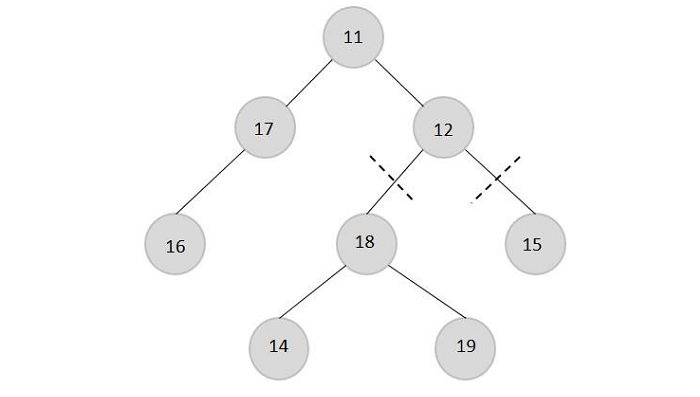
After the removal the three trees will be

• T1: {14, 18, 19}

• T2: {15},

• T3: {11,12,16,17}

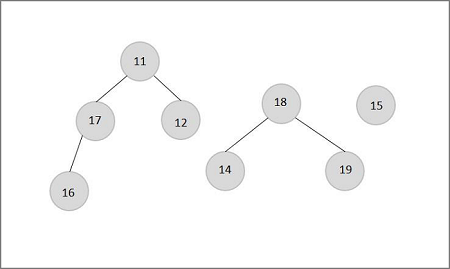
We can see that we got three trees and all the three nodes are in 3 different trees by disconnecting element two from the tree. The given C++ code shows that the Least Common Ancestor of nodes 18 and 15 is 12. So removing nodes at the top of 12 will not work. LCA of nodes 15 and 17 is 11, and LCA of nodes 18 and 17 is 11

As we observe,

• LCA(18, 15) = 12

• LCA(15, 17) =11

• LCA(18, 17) = 11

As we observe that one comes in both (15,17) and (18,17), deleting one will not work as the other two will still be connected. 12 is coming only once, and disconnecting this will disconnect both other nodes. Disconnecting this node will also disconnect the LCA of 11. These two were causing the same LCA, and now they have not connected themselves. If you are lost here, try to take an example and solve it yourself.

So all we need to do is find the LCA of all three nodes among themselves and take nonrepeating one,

Formally speaking, If −

LCA(a, b) = l

LCA(b, c) = m

LCA(a, c) = k

Then l==m, k is the answer, if m==k, then l is the answer and if l==k, then m is the answer.

Note − It's a bit tricky to wrap your head around this, so I recommend taking some examples and solving them yourself.

#include <iostream>
using namespace std;
class Node {
   public:
   int value;
   Node *left, *right;
   Node(int value) {
      this->value = value;
      left = right = NULL;
   }
};
Node* lca(Node* root, int key1, int key2) {
   if (root == NULL) {
      return NULL;
   }
   if (root->value == key1 || root->value == key2) {
      return root;
   }
   Node* llca = lca(root->left, key1, key2);
   Node* rlca = lca(root->right, key1, key2);
   if (llca && rlca) {
      return root;
   }
   return (llca != NULL) ? llca : rlca;
}
Node* solve(Node* root, int a, int b, int c) {
   Node* l = lca(root, a, b);
   Node* m = lca(root, b, c);
   Node* k = lca(root, c, a);
   if (l->value == m->value) {
      return k;
   }
   else if (l->value == k->value) {
      return m;
   }
   else {
      return l;
   }
}
int main() {
   Node* root = new Node(11);
   root->left = new Node(12);
   root->right = new Node(13);
   root->left->left = new Node(14);
   root->left->right = new Node(15);
   root->left->left->left = new Node(18);
   root->left->left->right = new Node(19);
   root->right->left = new Node(16);
   root->right->right = new Node(17);
   cout << "Disconnect node with value: " << solve(root, 18, 15, 17)->value;
   return 0;
}

Output

Disconnect node with value: 12

Conclusion