
- R - Home
- R - Overview
- R - Environment Setup
- R - Basic Syntax
- R - Data Types
- R - Variables
- R - Operators
- R - Decision Making
- R - Loops
- R - Functions
- R - Strings
- R - Vectors
- R - Lists
- R - Matrices
- R - Arrays
- R - Factors
- R - Data Frames
- R - Packages
- R - Data Reshaping
- R - CSV Files
- R - Excel Files
- R - Binary Files
- R - XML Files
- R - JSON Files
- R - Web Data
- R - Database
- R Charts & Graphs
- R - Pie Charts
- R - Bar Charts
- R - Boxplots
- R - Histograms
- R - Line Graphs
- R - Scatterplots
- R Statistics Examples
- R - Mean, Median & Mode
- R - Linear Regression
- R - Multiple Regression
- R - Logistic Regression
- R - Normal Distribution
- R - Binomial Distribution
- R - Poisson Regression
- R - Analysis of Covariance
- R - Time Series Analysis
- R - Nonlinear Least Square
- R - Decision Tree
- R - Random Forest
- R - Survival Analysis
- R - Chi Square Tests
- R Useful Resources
- R - Interview Questions
- R - Quick Guide
- R - Cheatsheet
- R - Useful Resources
- R - Discussion
R - Binomial Distribution
The binomial distribution model deals with finding the probability of success of an event which has only two possible outcomes in a series of experiments. For example, tossing of a coin always gives a head or a tail. The probability of finding exactly 3 heads in tossing a coin repeatedly for 10 times is estimated during the binomial distribution.
R has four in-built functions to generate binomial distribution. They are described below.
dbinom(x, size, prob) pbinom(x, size, prob) qbinom(p, size, prob) rbinom(n, size, prob)
Following is the description of the parameters used −
x is a vector of numbers.
p is a vector of probabilities.
n is number of observations.
size is the number of trials.
prob is the probability of success of each trial.
dbinom()
This function gives the probability density distribution at each point.
# Create a sample of 50 numbers which are incremented by 1. x <- seq(0,50,by = 1) # Create the binomial distribution. y <- dbinom(x,50,0.5) # Give the chart file a name. png(file = "dbinom.png") # Plot the graph for this sample. plot(x,y) # Save the file. dev.off()
When we execute the above code, it produces the following result −
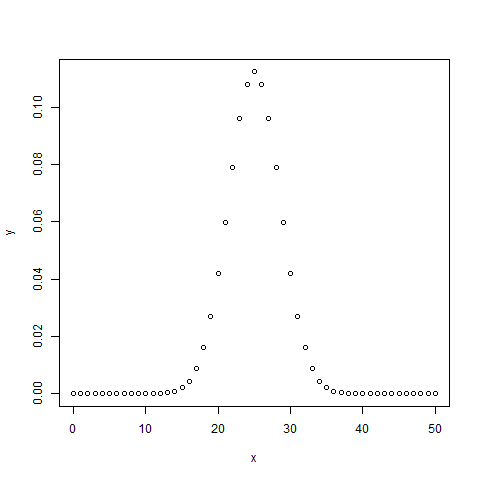
pbinom()
This function gives the cumulative probability of an event. It is a single value representing the probability.
# Probability of getting 26 or less heads from a 51 tosses of a coin. x <- pbinom(26,51,0.5) print(x)
When we execute the above code, it produces the following result −
[1] 0.610116
qbinom()
This function takes the probability value and gives a number whose cumulative value matches the probability value.
# How many heads will have a probability of 0.25 will come out when a coin # is tossed 51 times. x <- qbinom(0.25,51,1/2) print(x)
When we execute the above code, it produces the following result −
[1] 23
rbinom()
This function generates required number of random values of given probability from a given sample.
# Find 8 random values from a sample of 150 with probability of 0.4. x <- rbinom(8,150,.4) print(x)
When we execute the above code, it produces the following result −
[1] 58 61 59 66 55 60 61 67