Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Query for ancestor-descendant relationship in a tree in C++ Program
In this problem, we are given an N vertex tree and Q queries each consisting of two values i and j. Our task is to create a program to solve a Query for ancestor-descendant relationship in a tree.
To solve each query, we need to check whether the node i is the ancestor of node j in the tree.
Let’s take an example to understand the problem,
Input
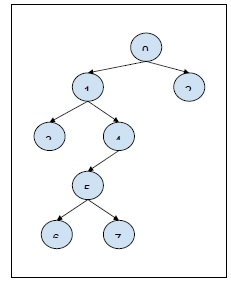
Q = 2, query[][] = {{3, 5}, {1, 6}}Output
No Yes
Explanation
i = 3, j = 5: The node 3 is not the ancestor of node 5. Return NO. i = 1, j = 6: The node 1 is the ancestor of node 6. Return YES.
Solution Approach
A solution to the problem is using tree traversing technique which is DFS (depth first Search). We will traverse from the ith node and do down to all its descendants and then check if the jth node is descendants of it. An efficient way to solve the problem is by finding out the time-in and time-out of each node. And check if they share ancestor-descendant relations.
Program to illustrate the working of our solution,
Example
#include <bits/stdc++.h>
using namespace std;
void depthFirstSearch(vector<int> g[], int u, int parent, int entTime[], int exitTime[], int& cnt){
entTime[u] = cnt++;
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (v != parent) depthFirstSearch(g, v, u, entTime, exitTime, cnt);
}
exitTime[u] = cnt++;
}
void calcTimeInAndOut(int edges[][2], int V, int entTime[], int exitTime[]){
vector<int> g[V];
for (int i = 0; i < V - 1; i++) {
int u = edges[i][0];
int v = edges[i][1];
g[u].push_back(v);
g[v].push_back(u);
}
int cnt = 0; depthFirstSearch(g, 0, -1, entTime, exitTime, cnt);
}
int main(){
int edges[][2] = { { 0, 1 }, { 0, 2 }, { 1, 3 }, { 1, 4 }, { 4, 5 }, { 5, 6 }, { 5, 7 }};
int E = sizeof(edges) / sizeof(edges[0]);
int V = E + 1;
int Q = 2;
int query[Q][2] = {{3, 5}, {1, 6}};
int entTime[V], exitTime[V];
calcTimeInAndOut(edges, V, entTime, exitTime);
for(int i = 0; i < Q; i++){
cout<<"For query "<<(i+1)<<" : "; (entTime[query[i][0]] <= entTime[query[i][1]] && exitTime[query[i][0]] <= exitTime[query[i][1]])? cout<<"is Ancestor\n":cout<<"is not Ancestor\n";
}
return 0;
}Output
For query 1 : is Ancestor For query 2 : is not Ancestor
135 Views
